Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.4 - Ex. 30
Em cada um dos problemas de 27 a 30, é dada uma função em um intervalo .
(a) Esboce os gráficos da extensão periódica par e da extensão periódica ímpar da função dada, ambas com período , em um intervalo de três períodos.
(b) Encontre as séries de Fourier em cossenos e em senos da função dada.
(c) Faça os gráficos de algumas das somas parciais de cada série.
(d) Para cada série, investigue a dependência em n do erro máximo em .
30.
Passo 1
(a) Fala galera!!
Nos foi dado a seguinte função:
Queremos esboçar os gráficos de uma extensão impar e de uma extensão par da função . Temos que Uma função é considerada par quando , qualquer que seja o valor de . Temos também que uma função é considerada ímpar quando , qualquer que seja o valor de .
Passo 2
A função dada é definida para um período de intervalo . Para a extensão par desta função, podemos definir uma função do período de intervalo tal que:
Ou seja, para a função onde , temos que:
Reescrevendo como uma função temos:
Agora, podemos plotar o gráfico para um intervalo de 3 período da função que representa a extensão par da função . Assim temos:
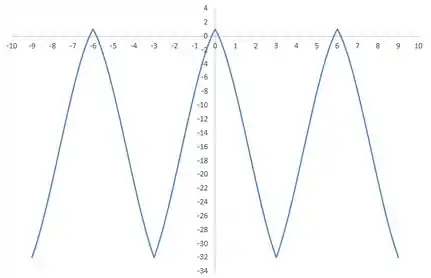
Passo 3
A função dada é definida para um período de intervalo . Com em uma função impar
Ou
Assim, para uma extensão impar desta função, podemos definir uma função do período de intervalo tal que:
Ou seja, para a função , temos que:
Reescrevendo como uma função temos:
Agora, podemos plotar o gráfico para um intervalo de 3 período da função que representa a extensão impar da função . Assim temos:
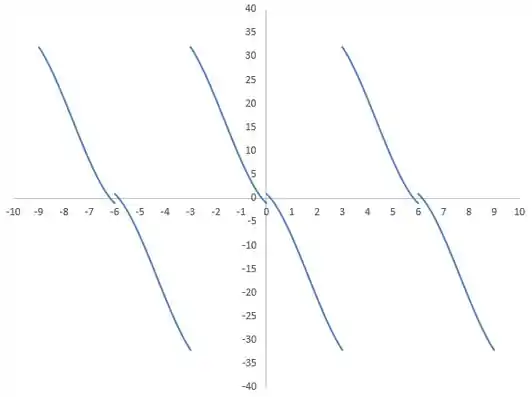
Passo 4
(b) Queremos encontrar os coeficientes e para as series em cosseno e seno das extensões par e impar para um período da função . Então, vamos calcular o coeficiente . Para isso, podemos usar a seguinte relação fornecida no livro:
Assim, temos que a extensão par pode ser dada como uma série de Fourier da seguinte forma:
Passo 5
Então, temos que é o seguinte:
Por integração por partes, temos o seguinte:
Temos que sempre será , temos também que e .
Passo 6
Podemos calcular da seguinte maneira:
Passo 7
Substituindo, os termos encontrados na relação fornecida no passo 4, temos que a série de Fourier para um a extensão par de é a seguinte:
Passo 8
Agora, vamos calcular o coeficiente . Para isso, podemos usar a seguinte relação fornecida no livro:
Assim, temos que a extensão impar pode ser dada como uma série de Fourier da seguinte forma:
Passo 9
Então, temos que é o seguinte:
Por integração por partes, temos o seguinte:
Temos que sempre será , temos também que e .
Passo 10
Substituindo, os termos encontrados na relação fornecida no passo 8, temos que a série de Fourier para uma extensão impar de é a seguinte: