Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.4 - Ex. 22b
Diferencie a Eq. (i) em relação a r e mude as ordens das derivadas em relação a r e a t, mostrando, assim, que
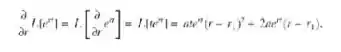
Como a última expressão à direita na Eq. (ii) é zero quando r = r1, conclua que t exp(r1t) também é solução de L[y] = 0.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a solução para a equação. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser pensar que, por ser linear e homogênea, teremos a solução no seguinte formato:
Passo 3
Pronto!! Agora é só substituir os valores e achar a solução!!
Resposta
Exercícios de Livros Relacionados
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. 1 - x 2 y ' ' - 2 x y ' = 0 ;y 1 =
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. 1 - 2 x - x 2 y ' ' + 2 1 + x y '
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. 4 x 2 y ' ' + y = 0 ;y 1 = x 1 2 l
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. x 2 y ' ' - x y ' + y = 0 ;y 1 = x
Nos problemas 1-30, encontre uma segunda solução para cada equação diferencial. Use redução de ordem ou a fórmula (4) como ensinada. Suponha um intervalo apropriado. x 2 y ' ' - 3 x y ' + 5 y = 0 ;y 1