Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 75
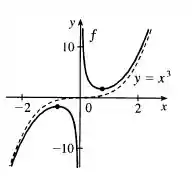
Discuta o comportamento assintótico de da mesma forma que no Exercício . Use então seus resultados para auxiliá-lo no esboço do gráfico .
Passo 1
Bom galera, nessa questão queremos mostrar que a função
possui assíntota oblíqua.
Para isso, iremos utilizar o seguinte limite
Onde é a equação da assíntota oblíqua.
Iremos utilizar os conceitos desse capítulo para tirar conclusões a respeito do gráfico de , que são basicamente:
Primeira derivada
Quando a primeira derivada é positiva a função cresce
Quando ela é negativa a função decresce
E quando ela troca de sinal a função possui um valor extremo que é máximo quando ela troca de positiva para negativa (crescia, chega no máximo e depois decresce). E que é mínimo quando ela troca de negativa para positiva (decrescia, chega no mínimo e depois cresce).
Segunda derivada
Quando a segunda derivada é positiva a função é côncava para cima
Quando ela é negativa a função é côncava para baixo
E quando ela troca de sinal a função possui um ponto de inflexão.
Passo 2
Podemos escrever a nossa função como:
Repare que o termo tende a zero quando tende a infinito:
Dessa forma, como queremos encontrar uma função que respeite:
Temos que:
Um bom indicativo portanto que:
E de fato se fizermos:
Dessa forma, é uma assíntota oblíqua de .
Passo 3
Derivando em relação a , temos
Fazendo um estudo de sinais temos:
Tirando a raíz quarta e usando o módulo pois a raíz possui índice par, temos:
De forma que:
E
Como para , então nossa função está crescendo em e e decrescendo em e .
Perceba que não está no domínio da nossa função pois teríamos uma divisão por zero.
A função possui máximo local em , pois antes desse ponto a função cresce e depois dele a função decresce.
A função possui mínimo local em , pois antes desse ponto a função decresce e depois dele a função cresce.
Passo 4
Derivando em relação a , temos
Avaliando o sinal dessa segunda derivada temos que se , todos os termos são positivos e portanto:
E se , todos os termos são negativos e portanto:
Como para , então nossa função possui concavidade para cima em e concavidade para baixo em . A função possui valores de mínimo local em e valores de máximo local em . A função não possui pontos de inflexão.
Passo 5
Reunindo essas informações, podemos tentar esboçar um gráfico que vai ser bem parecido com esse daqui:
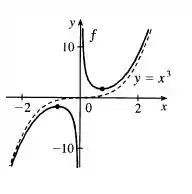
Resposta
