Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.5 - Ex. 76
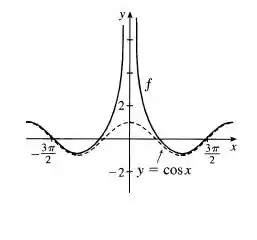
Use o comportamento assintótico de para esboçar seu gráfico sem seguir o roteiro de esboço de curvas desta seção.
Passo 1
Bom galera, nessa questão queremos mostrar que a função possui uma assíntotas oblíqua. Para isso, iremos utilizar o seguinte limite
Onde é a equação da assíntota oblíqua.
Passo 2
Para mostrar o comportamento assintótico de , iremos resolver o seguinte limite
Dessa forma, o gráfico é assintótico em .
Passo 3
Podemos ver que
Dessa forma, é uma assíntota vertical. Não é necessário calcular as derivadas e verificar pontos de inflexão e de máximo e mínimo, como determinado na questão, pois sabemos o comportamento assintótico de .
Resposta
Exercícios de Livros Relacionados
Discuta o comportamento assintótico de f x = ( x 4 + 1 ) / x da mesma forma que no Exercício 70 . Use então seus resultados para auxiliá-lo no esboço do gráfico f .
Mostre que a curva y = x - tan - 1 x tem duas assíntotas oblíquas: y = x + π / 2 e y = x - π / 2 . Use esse fato para esboçar a curva.
Seja f x = x 3 + 1 / x . Mostre que lim x → ± ∞ f x - x 2 = 0 Isso mostra que o gráfico de f tende ao gráfico de y = x 2 , e dizemos que a curva y = f ( x ) é assintótica à parábola y = x 2 . Use es
Use o roteiro desta seção para esboçar o gráfico da curva. No passo D , ache uma equação para a assíntota oblíqua. y = 2 x 3 + x 2 + 1 x 2 + 1
Use as assíntotas de f x = sin x + e - x para esboçar o gráfico sem recorrer ao procedimento desta seção.