Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 68
- Qual é a distância mínima de um ponto da semicircunferência ao ponto ?
- Trace o gráfico da função distância juntamente com o de e concilie o que você observa com a resposta do item (a)
Passo 1
Sabemos que para calcular a distância entre dois pontos e , por exemplo, devemos fazer ). Bom, para evitarmos trabalhar com raiz quadrada vamos trabalhar com a função que é o quadrado da distância e, por fim, vamos tirar a raiz quadrada do ponto de mínimo encontrado em para encontrarmos o valor dessa distância mínima.
Passo 2
Qualquer ponto que pertencer a semicircunferência é caracterizado como sendo do tipo . Dessa forma, precisamos encontrar a distância entre os pontos e e faremos isso utilizando a nossa função “quadrado da distância” ().
Derivando essa função para acharmos os pontos críticos () que são nossos candidatos a pontos de mínimo/máximo. Assim,
Elevando ambos os lados ao quadrado, teremos
Podemos descartar pelo fato não convir com a situação problema. Tomemos, então, e analisaremos a derivada nas proximidades desse ponto. Podemos reparar que no intervalo e em , portanto, o ponto em análise é um ponto de mínimo.
Por fim, para calcularmos o valor da distância mínima, basta fazermos , mas primeiro precisamos calcular o valor de da seguinte forma
Finalmente, a nossa distância mínima será dada por
Passo 3
Plotando os 2 gráficos obtemos
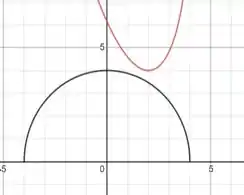
A distância mínima do ponto ao ponto no gráfico de ocorre quando e nossa função assume seu valor mínimo.
Resposta
Ei, a resposta está no passo a passo :)