Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 15
- Quantas soluções a equação possui?
- Use o método de Newton para determiná-las.
Passo 1
Usaremos o método de Newton que nos diz que
Para obtermos aproximações para as raízes da equação dada.
Passo 2
Plotando e equação obtemos o seguinte gráfico
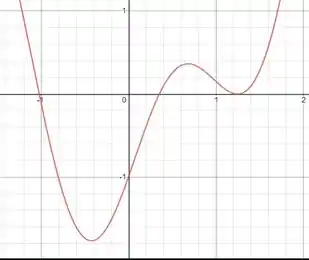
Aparentemente temos duas raízes, no entanto, dando um zoom nas proximidades de vemos que o gráfico não toca o eixo.Portanto, temos duas raízes.
Passo 3
Para estimar onde estão essas raízes utilizaremos os pontos iniciais e que são próximos das raízes pelo gráfico. Primeiramente vamos derivar a função para podermos aplicar a fórmula do método de Newton.
Assim ficaremos com
Substituindo os valores de na fórmula acima, lembrando-se que cada valor de nos fornecerá uma aproximação pra raiz obteremos as seguintes aproximações : .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja f x = 3 x - x 3 . Mostre que a equação f x = - 4 tem uma solução no intervalo [2,3] e use o método de Newton para determiná-la.
Deduza o método de Newton a partir de sua interpretação geométrica.
Aplique o método de Newton-Raphson à equação: x 3 - 2 x 2 - 3 x + 10 = 0 com x 0 = 1.9 . Justifique o que acontece.
Encontre uma raiz da equação: p ( x ) = x 4 - 6 x 3 + 10 x 2 - 6 x + 9 = 0 , aplicando o método de Newton para polinômios.
Use o método de Newton-Raphson para obter a menor raiz positiva das equações a seguir com precisão ϵ = 1 0 - 4 x 2 - t g ( x ) = 0 2 c o s ( x ) = e x 2 x 5 - 6 = 0