Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 66

a. A função y = t g x + 3 c o t g x possui um valor mínimo absoluto no intervalo 0 < x < π 2 . Determine-o.

b. Esboce o gráfico da função e compare o que você observa com a resposta do item (a).

Passo 1

O exercício nos afirma que a função tem um ponto de mínimo absoluto dentro do intervalo 0 < x < π 2 e pede para que determinemos quem ele é, depois o problema nos pede para plotarmos o gráfico de y = f ( x ) e compararmos com o que achamos no item (a).

Passo 2

Peguemos nossa função y = t g x + 3 c o t g x e a derivemos

f ' x = sec 2 ⁡ x - 3 c o s s e c 2 x

Para encontrarmos os pontos críticos, candidatos a máximo ou mínimo, façamos f ' x = 0

sec 2 ⁡ x - 3 c o s s e c 2 x = 0

sec 2 ⁡ x = 3 c o s s e c 2 x

1 cos 2 ⁡ x = 3 ⋅ 1 s e n 2 x

t g 2 x = 3

Para o intervalo de 0 < x < π 2 temos t g x > 0 . Assim,

t g x = 3

→ x = π 3

Analisando a segunda derivada da nossa função f x = y temos

f " ( x )   =   2 s e c ² ( x ) ⋅ t g ( x )   +   6 c o s s e c ² ( x ) ⋅ c o t g ( x )

Para qualquer valor no intervalo dado f " ( x )   > 0 . Portanto x = π 3 é ponto de mínimo absoluto dentro do intervalo e o mínimo valor de y = f x é y = 2 3 .

Passo 3

O esboço do gráfico fica sendo

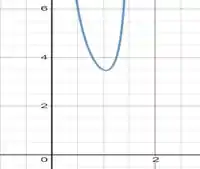
O gráfico confirma o que foi encontrado no item a.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

60. Como tossimos. a. Quando tossimos, a traqueia se contrai e aumenta a velocidade do ar que passa. Isso levanta questões sobre quanto ela deveria se contrair para maximizar a velocidade e se ela rea
50. Trajetória de aterrissagem de um avião. Um avião que voa à altitude H começa a descer rumo à pista de pouso de um aeroporto que está a uma distância terrestre horizontal L do avião, como mostra a
53. Fórmula do tamanho do lote de Wilson. Uma das fórmulas para gerenciamento de almoxarifado diz que o custo médio semanal para você encomendar, pagar e armazenar uma mercadoria é: A q = k m q + c m
Ache a altura do Cone circular reto com maior volume que pode ser inscrito numa esfera de raia a.
Um cone circular reto deve ser inscrito em uma esfera com um dado raio. Ache a razão entre a altura e o raio da base do cone de maior volume possível.