Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 61

Duas cidades A e B devem receber seu suprimento de água da uma estação de tratamento situada à margem de um rio, com um curso em linha reta que está a 15 km de A e a 10 km de B . Se os pontos do rio mais próximos de A e B estão separados por 20 km e A e B estão do mesmo lado do rio, onde a estação deveria estar situada, de modo que o mínimo de canos fossem empregados.

Passo 1

Esse é um problema que precisa de um esboço para resolver. Veja abaixo o esboço do problema com os dados da questão, a reta que passa por C e P representa a margem do rio e P a estação.

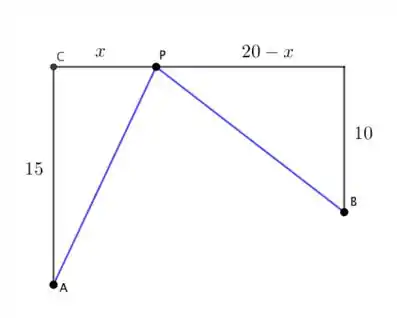
Os canos são representados pelos segmentos A P ¯ e P B ¯ . Então devemos descobrir o valor mínimo de C = A P ¯ + P B ¯ .

Passo 2

Vamos achar a expressão de A P ¯ e P B ¯ . Podemos utilizar os triângulos retângulos formados. Dessa forma,

A P ¯ 2 = x 2 + 15 2   →       A P ¯ = x 2 + 225

e

P B ¯ 2 = ( 20 - x ) 2 + 10 2   →       P B ¯ = ( 20 - x ) 2 + 100

Logo, o comprimento dos canos é dado pela função:

C x = x 2 + 225 + ( 20 - x ) 2 + 100                 x ∈ [ 0,20 ]

Passo 3

Agora nós vamos derivar e igualar a 0 para descobrir os pontos críticos.

C ' x = 2 x 2 x 2 + 225 + 2 ( 20 - x ) ( - 1 ) 2 ( 20 - x ) 2 + 100

C ' x = x x 2 + 225 - 20 - x ( 20 - x ) 2 + 100

x x 2 + 225 - 20 - x 20 - x 2 + 100 = 0

x x 2 + 225 = 20 - x 20 - x 2 + 100       →         x x 2 + 225 2 = 20 - x 20 - x 2 + 100 2  

x 2 x 2 + 225 = 20 - x 2 20 - x 2 + 100       →           x 2 + 225 - 225 x 2 + 225 = 20 - x 2 + 100 - 100 20 - x 2 + 100

1 - 225 x 2 + 225 = 1 - 100 20 - x 2 + 100   →           225 x 2 + 225 = 100 20 - x 2 + 100

x 2 + 225 225 = 20 - x 2 + 100 100       →         x 2 225 + 1 = 20 - x 2 100 + 1

x 2 15 2 = 20 - x 2 10 2     →         x 15 = 20 - x 10     →     10 x = 300 - 15 x   →     25 x = 300

x = 12

Como C é contínua em [ 0,20 ] o mínimo absoluto ocorre nos extremos do intervalo ou no ponto crítico x = 12 .

Passo 4

Agora vamos decidir qual vai ser o mínimo absoluto.

C 12 = 12 2 + 225 + ( 20 - 12 ) 2 + 100 = 369 + 164 = 3 41 + 2 41 = 5 41

C 12 = 5 41 ≈ 32,02

C 20 = 20 2 + 225 + ( 20 - 20 ) 2 + 100 = 625 + 10 = 25 + 10 = 35

C 20 = 35

C 0 = 0 2 + 225 + ( 20 - 0 ) 2 + 100 = 15 + 500 = 15 + 10 5

C 0 = 15 + 10 5 ≈ 37,36

Como podemos observar, o mínimo ocorre quando x = 12 . Logo, a estação devera estar a 12   km do ponto C .

Resposta

A estação deverá estar situada a 12   km do ponto, na margem do rio, mais próximo da cidade A .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache dois números não-negativos cuja soma seja 12 e tais que a soma de seus quadrados seja um mínimo absoluto.
Numa cidade com 11.000 habitantes, a taxa de crescimento de uma epidemia é diretamente proporcional ao produto dos números de pessoas infectadas e não-infectadas. Determine o número de pessoas infecta
Ache dois números não-negativos cuja soma seja 12 e tais que seu produto seja um máximo absoluto.
Uma lata fechada com um volume de 27 c m 3 deve ter a forma de um cilindro circular reto. Se a tampa e a base, ambas circulares, forem cortadas de pedaços quadrados de lata, ache o raio e a altura da