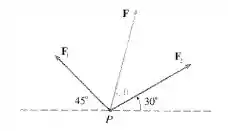
Duas forças e com grandezas 10 lb e 12 lb agem sobre um objeto em um ponto P como mostrado na figura. Determine a força resultante agindo em P assim como sua magnitude, direção e sentido. (Indique a direção determinando o ângulo ) exposto na figura.

Vamos assumir aqui que a direção horizontal para direita é a direção positiva do eixo e que a direção vertical para cima é a direção positiva do eixo . Portanto, precisamos decompor as duas forças nestas duas direções.

Para realizarmos esta decomposição, vamos utilizar as relações angulares. Portanto,

Agora, vamos somar os dois vetores, somando coordenada a coordenada. Logo,

Para calcularmos a sua magnitude, basta tirarmos a norma do vetor. Logo,

E a sua direção e sentido é dado pelo ângulo , que é expresso por: