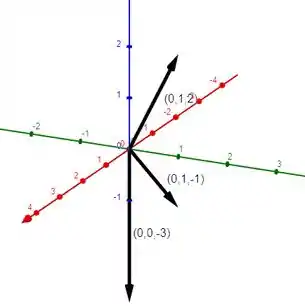
Determine a soma dos vetores dados e ilustre geometricamente.
Passo 1
Precisamos fazer duas operações: soma de vetores e esboça-los.
Para soma-los, basta somar coordenada a coordenada. Portanto, o vetor será dado por:
Passo 2
Vejamos agora a representação gráfica de cada um desses vetores! Colocando-os partindo do mesmo ponto, a origem, temos:
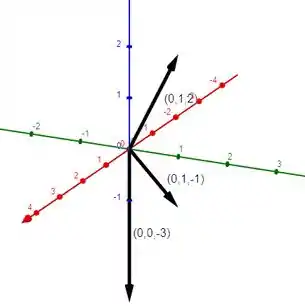
Apesar destes vetores estarem contidos em um mesmo plano (plano ), deve-se esboça-los no , pois estamos falando de três dimensões!
Resposta
Vetor resultante:
Graficamente, temos: