Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.4 - Ex. 30

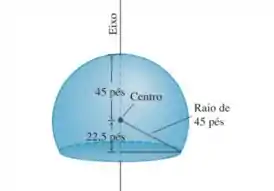
Eis um desenho esquemático da redoma de 90 pés usada pelo Serviço Nacional de Meteorologia dos Estados Unidos para abrigar um radar em Bozeman, Montana.

  1. Qual é a área da superfície externa a ser pintada (sem contar a base)?
  2. Arredonde a resposta para p é 2 mais próximo.

Passo 1

  1. Para essa questão podemos calcular a área da curva x = 45 2 - y 2 (equação do círculo) em torno do eixo y , considerando os limites de integração como - 22,5   e   45 . A área da superfície gerada ao rotacionar a curva em torno do eixo x é dada por:

    2. S = ∫ a b 2 π g y 1 + g ' y 2   d y

    Assim, temos que:

    S = ∫ - 22,5 45 2 π 45 2 - y 2   1 + - y 45 2 - y 2 2 d y =  

    =   2 π ∫ - 22,5 45 45 2 - y 2   45 2 - y 2 + y 2 45 2 - y 2   d y = 2 π ∫ - 22,5 45 45   d y = 90 π y 45 - 22,5 =

    = 90 π 45 - - 22,5 = 90 π × 67,5 = 6075   π   f t 2

    Passo 2

  2. 6075 × 3,1416 = 19085,17   f t 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da superfície do tronco de cone gerado pela rotação do segmento de reta y = x 2 + 1 2 , 1 ≤ x ≤ 3 , em torno do eixo x . Verifique se sua resposta coincide com a fórmula geométrica. Á
Determine a área da superfície do tronco de cone gerado pela rotação do segmento de reta y = x 2 + 1 2,1 ≤ x ≤ 3 , em torono do eixo y . Verifique se seu resultado coincide com a fórmula geométrica: Á
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. y = x 3 9 , 0 ≤ x ≤ 2 ;e i x ox
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. y = x ,3 4 ≤ x ≤ 15 4 ;e i x ox
Determine a área da superfície gerada pela rotação da curva em torno do eixo indicado. y = 2 x - x 2 ,0,5 ≤ x ≤ 1,5 ;e i x ox