Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.2 - Ex. 23

Mostre que função g t = t + 1 + t - 4 , tem exatamente uma raíz no interior do intervalo (0, ∞ ).

Passo 1

Haja vista que um polinômio de grau n pode apresentar n raízes reais queremos mostrar que no intervalo (- ∞ , 0) a função   g x dada tem exatamente uma raiz, para isso contaremos com o auxílio da análise gráfica da derivada.

Passo 2

Tomemos nossa função g t = t + 1 + t - 4 e a derivemos:

g ' x = 1 2 t + 1 2 1 + t

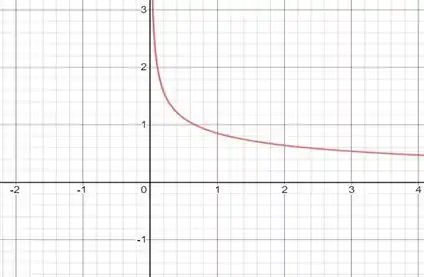
Passo 3

A partir da observação do gráfico acima percebemos que a função g ' ( x ) > 0 no intervalo (0, ∞ ) o que implica que g x está crescendo no mesmo intervalo.

Passo 4

Vamos, agora, testar valores inteiros próximos de onde a função g ' x começa a decrescer de forma um pouco mais acentuada. Tomemos os inteiros 3 e 4, por exemplo. g 3 = 3 +   3 + 1 - 4

g 3 = 3 +   4 - 4

g 3 = 3 +   2 - 4

g 3 = 3 - 2   < 0 P a r a   o   4   t e r e m o s :

g 4 = 4 + 4 + 1 - 4

g 4 = 4 + 5 - 4

g 4 = 2 + 5 - 4

g 4 = 5 - 2 > 0

Passo 5

Como temos g 3 < 0   e   g 4 > 0 pelo teorema do valor intermediário sabemos que existe uma raiz nesse intervalo e como g ( x ) tende a crescer quando os valores de x tendem ao infinito, podemos concluir que existe exatamente uma raiz nesse intervalo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que função r( θ ) = 2 θ - cos 2 ⁡ θ + 2 , tem exatamente uma raiz no interior do intervalo (- ∞ , ∞ ).
Mostre que função r( θ ) = θ + sen ² ⁡ θ 3 - 8 ² , tem exatamente uma raíz no interior do intervalo (- ∞ , ∞ ).
Determine todas as funções possíveis com a derivada y ' =1 x .
Determine todas as funções possíveis com a derivada y ' = sec 2 ⁡ θ . y ' = θ y ' = θ - sec 2 ⁡ θ
Determine todas as funções possíveis com a derivada y ' = 1 - 1 x 2 .