Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 13
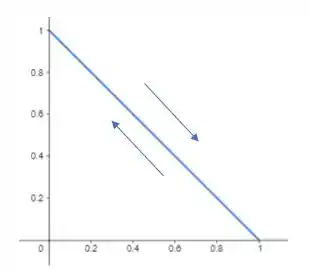
a) Elimine o parâmetro para encontrar uma equação cartesiana da curva.
b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Oii!!! Bom... O problema fornece um curva na forma parametrizada e pede para encontrarmos uma equação cartesiana que relacione e .
Neste caso, temos
E
Para isso, podemos relacionar as equações que o enunciado nos deu com alguma relação trigonométrica que já conhecemos, como, por exemplo:
Em seguida, depois que descobrirmos a expressão que queremos, basta esboçarmos e analisarmos o que acontece com e quando alteramos o valor de .
Agora bora lá!! 😉
Passo 2
Assim, da relação fundamental da trigonometria, temos:
Portanto, isolando :
Veja que essa equação trata-se de uma reta, mas você deve tomar um cuidado: não é a reta toda! Sabemos que . Assim,
A curva é o pedaço da reta com entre e .
Passo 3
Fazendo um esboço da curva, temos:
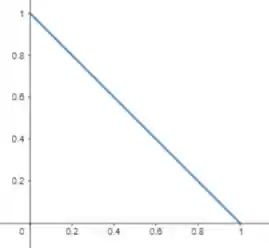
Agora vamos aplicar alguns valores de e observar os valores de e :
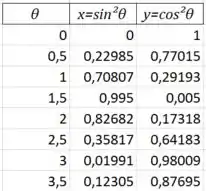
Perceba que, conforme aumenta, como as funções trigonométricas são periódicas, os pontos vão indo e voltando na reta!
Com isso, o crescimento em relação ao parâmetro fica da seguinte forma:
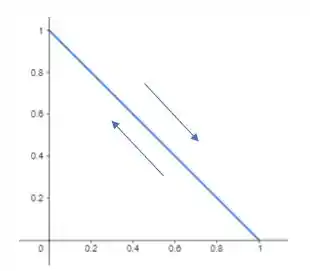
Resposta
