Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 12
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
a) Nesta questão temos que eliminar o parâmetro encontrar a equação cartesiana da curva dada paramétricas e no intervalo de , podemos utilizar as identidades trigonométicas para substituir e em termos de e .
Dadas as equações:
Colocamos e em evidencia
Passo 2
Vamos lembrar da identidade trigonométrica , e substituir os termos.
Temos então uma equação caracterisrica da elipse.
Passo 3
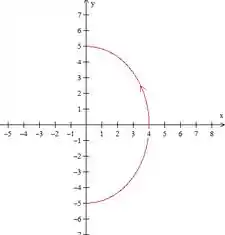
Na letra (B) temos que construir a curva e indicar a diração quando o parâmetro aumenta.
Esta é a equação de uma elipse com semieixos maior e menor de comprimento e , respectivamente, centrada na origem do sistema de coordenadas cartesianas.
Porém, o intervalo de parametrização é:
Portanto não estamos falando da elipse inteira, apenas de metade dela. (é como se o intervalo fosse de até )
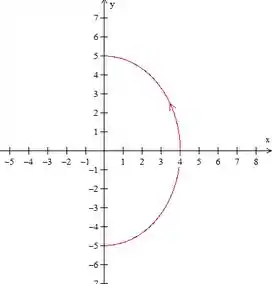
Passo 4
Para descobrirmos o aumento iremos substituir o intervalo nas equações de e .
Quando temos
Quando temos
Resposta
Quando temos
Quando temos
Assim, nossa semicircunferência começa no ponto e termina no ponto .
Além disso, nesse intervalo de temos que
Então
E nossa semielipse está na parte positiva do eixo .
Resposta
