Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 3
Encontrar a área da superfície do cilindro limitada pelos planos , , , .
Passo 1
De maneira simples, temos que lembrar que o cálculo da área de uma superfície é dada por
Assim precisamos apenas conhecer nossa funções e nossos limites de integração.
Passo 2
Nossa função já foi dada, entretanto precisamos fazer uma parametrização que nos ajude a trabalhar melhor nossa integração.
Vamos fazer
Assim temos que
Isso nos da
Tirando o produto vetorial entre nossos dois vetores, temos
E a norma do nosso vetor é
Agora só nos falta definir os intervalos de integração. Para isso vamos olhar os planos que nos limitam. Primeiro Vamos ver as limitações na direção , onde temos que nosso intervalo se limita entre e . Agora na direção temos que olhar para .
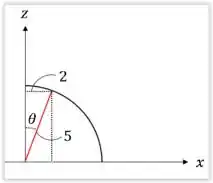
Observando a imagem, temos que nosso se limita entre e . Assim estamos prontos para começar a integrar nosso problema.
Passo 3
Nossa integral pode ser escrita como
Agora vamos resolver e vê no que dá.
Integrando na direção , temos algo bastante simples.
Entretanto eu só calculei a metade do que eu realmente queria. Logo temos que a área total será