Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 8
Calcular a área da parte da esfera interior ao cilindro
Passo 1
De maneira simples, temos que lembrar que o cálculo da área de uma superfície é dada por
Assim precisamos apenas conhecer nossa funções e nossos limites de integração.
Passo 2
Não estamos construindo o Frankenstein, mas vamos por partes. Primeiro tome nossa função
Tendo assim como derivadas direcionais
e
Conhecendo nossas derivadas, podemos determinar que o fator de integração se resume em
Vamos usar coordenadas cilindras para nos ajudar a entender melhor nossas limitações, assim temos.
Assim nossa integral se transforma
Entretanto ainda precisamos entender como nosso cilindro este disposto.
Um cilindro de dentro no plano e raio 2.
Onde temos
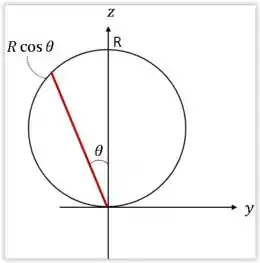
Onde é o raio da esfera.
Passo 3
Vamos integrar?
Para a primeira parte, vamos fazer
Assim temos
Lembrando que
Que é apenas a parte que está em assim temos que a área total é o dobro o que encontramos, ficando com