Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.2 - Ex. 30

Encontre f ' ( x ) e f^(' ') (x) :

30) f ( x ) = (x)/(x ² - 1)

Passo 1

Bom, precisamos derivar esta função. Antes de tudo devemos notar que há uma divisão entre os termos. Então o que usamos?

A Regra do Quociente, certo? Vamos lembrar:

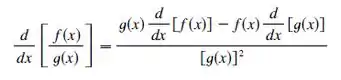
Se chamarmos:

f (x) = x

g (x) = x ² - 1

Derivando:

(d)/(d x) f (x) = 1

(d)/(d x) g (x) = 2 x

Substituindo:

(d)/(d x) [(f (x))/(g (x))] = ((x^2 - 1) (1) - x ( 2 x ))/((x^2 - 1)^2)

Então:

(d)/(d x) [(f (x))/(g (x))] = (x^2 - 1 - 2 x ²)/((x^2 - 1)^2) = (- (x^2 + 1))/((x^2 - 1)^2)

Vamos manipular um pouquinho isto aqui:

(d)/(d x) [(f (x))/(g (x))] = - ((x^2 + 1))/((x^2 - 1)^2)

Achamos a derivada primeira, agora precisamos da derivada segunda!

Passo 2

Agora temos uma nova função:

f ' ( x ) = (- (x^2 + 1))/((x^2 - 1)^2)

Também possui uma razão entre as funções, então vamos resolver da mesma maneira que f (x) .

Chamamos:

f (x) = - x^2 - 1

g (x) = (x^2 - 1)^2

Derivando:

(d)/(d x) f (x) = - 2 x

(d)/(d x) g (x) = 2 (x^2 - 1) (2 x) = 4 x (x^2 - 1)

Substituindo:

(d)/(d x) [(f (x))/(g (x))] = (((- 2 x) (x^2 - 1)^2 - (4 x (x^2 - 1)) (- x^2 - 1)))/(((x^2 - 1)^2)^2)

f^(' ') (x) = (- 2 x (x^4 - 2 x^2 + 1) - 4 x (- x^4 - x^2 + x^2 + 1))/((x^2 - 1)^4)

f^(' ') (x) = (- 2 x^5 + 4 x^3 - 2 x - 4 x (1 - x^4))/((x^2 - 1)^4)

f^(' ') (x) = (- 2 x^5 + 4 x^3 - 2 x - 4 x + 4 x^5)/((x^2 - 1)^4)

f^(' ') (x) = (2 x^5 + 4 x^3 - 6 x)/((x^2 - 1)^4)

Resposta

f ' ( x ) = - ((x^2 + 1))/((x^2 - 1)^2)

f^(' ') (x) = (2 x^5 + 4 x^3 - 6 x)/((x^2 - 1)^4)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

determiney ' (a) pela aplicação da regra do produto e (b) pela multiplicação dos fatores para produzir uma soma de termos mais simples para derivar. y = 3 - x 2 x 3 - x + 1
Determine a derivada das funções abaixo:22 - (2 x - 7)^(- 1) * (x + 5)
determiney ' (a) pela aplicação da regra do produto e (b) pela multiplicação dos fatores para produzir uma soma de termos mais simples para derivar. y=( 1 + x 2 ) ( x 3 / 4 - x - 3 )
Determine a derivada da funçãof (s) = (sqrt(s) - 1)/(sqrt(s) + 1)
Determine a derivada da funçãoy = x^3 e^x