Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.2 - Ex. 39
- Se , encontre e .
- Verifique se sua resposta em (a) é razoável, comparando os gráficos de , e .
Passo 1
Bom, precisamos derivar esta função. Antes de tudo devemos notar que há uma divisão entre os termos. Então o que usamos?
A Regra do Quociente, certo? Vamos lembrar:
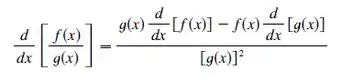
Se chamarmos:
Derivando:
Substituindo:
Se isolarmos :
Então:
Passo 2
Agora temos uma nova função:
Também possui uma razão entre as funções, então vamos resolver da mesma maneira que
Chamamos:
Derivando:
Substituindo:
Então:
Ou seja:
E pronto! Terminamos a letra a, e agora vamos para a b!
Passo 3
Desenhando o gráfico, onde verde representa f, laranja f’ e rosa f’’:
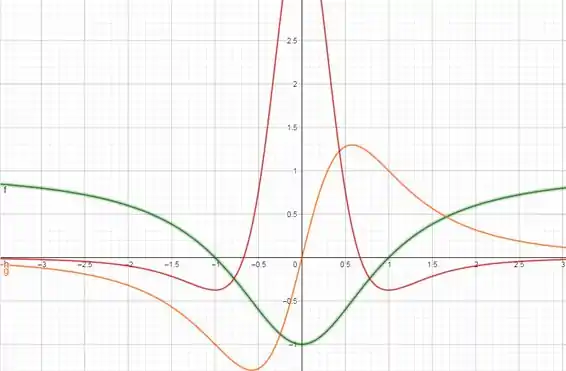
A derivada primeira nos mostra a inclinação da reta tangente ao gráfico da função. Então, pelo gráfico, quando a derivada é positiva, a reta tangente tem inclinação crescente e, consequentemente, a função também cresce. Quando a inclinação diminui, a função decresce. Quando a derivada primeira é zero, a reta tangente possui inclinação horizontal naquele ponto!
Quando a derivada segunda é igual a zero, a derivada primeira possui uma inclinação tangente horizontal. A mesma análise pode ser feita para a derivada segunda, já que quando a derivada é positiva, a reta tangente tem inclinação crescente e, consequentemente, a função também cresce. Quando a inclinação diminui, a função decresce.
Com relação à função, quando f’’ é negativo o gráfico é côncavo para baixo e côncavo para cima quando f’’ é positivo.