Exercícios de Regra do Produto e do Quociente - Lista de Exercícios Resolvida
Questão 9
Calcule a derivada das seguintes funções, usando as regras de derivação:
Ver solução completa
Questão 12
Seja o único número real tal que a reta tangente ao gráfico de no ponto passa pelo ponto . Então o valor de vale quanto?
Ver solução completaQuestão 13
Calcule a derivada das seguintes funções, usando as regras de derivação:
Ver solução completaQuestão 14
Derive cada função (se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 18
Sejam e duas curvas no espaço . Mostrar que, para o produto escalar
vale a regra de derivação
Ver solução completaQuestão 19
3a) Calcule, usando as regras de derivação, as derivadas das seguintes funções:
Ver solução completaQuestão 21
09) Derive a função. (Se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 30
Encontre a derivada das funções abaixo de duas formas (aplicando diretamente uma regra ou simplificando/multiplicando primeiro e aplicando outra regra) e verifique que o resultado é o mesmo
Questão 33
3) Sejam e funções diferenciáveis tais que
-
-
-
Para todo . O valor de é
Escolha uma:
A.
B.
C.
D.
E.
Ver solução completaQuestão 46
4) Sejam , e funções diferenciáveis definidas em . Sabe-se que e para todo valor inteiro .
O valor de é
Escolha uma:
A.
B.
C.
D.
E.
Ver solução completaQuestão 47
3) Sejam , e funções diferenciáveis em . Sabe-se que , e .
O valor de é
Escolha uma:
A.
B.
C.
D.
E.
Ver solução completaQuestão 48
Calcule ou argumente que os valores não existem. Em todos os casos justifique seus cálculos e respostas.
Derivada de em .
Ver solução completaQuestão 49
Questão 2) Calcule a derivada das seguintes funções, usando as regras de derivação:
b)
Ver solução completaQuestão 51
Questão 3:
Use a regra de derivação e calcule a função derivada em cada caso.
a)
Ver solução completaQuestão 52
Questão 3:
Use a regra de derivação e calcule a função derivada em cada caso.
b)
Ver solução completaQuestão 54
O movimento de uma mola sujeita a uma força de atrito é frequentemente modelado pelo produto de uma função exponencial e uma função seno. Suponha que a equação do movimento de um ponto sobre essa mole é:
em que s é medida em centímetros e t em segundos.
Encontre a velocidade após t segundos.
Ver solução completaQuestão 59
3b) Calcule, usando as regras de derivação, as derivadas das seguintes funções:
Ver solução completaQuestão 61
Q02a) Usando as regras de derivação, calcule a derivada das seguintes funções:
Ver solução completaQuestão 62
Q02b) Usando as regras de derivação, calcule a derivada das seguintes funções:
Ver solução completaQuestão 66
Considere a função . Indique qual a opção abaixo para .
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 69
Seja uma função derivável e um número positivo.
- Use a regra do quociente para provar que
- Use o item anterior para mostrar que
Questão 72
Questão 4 - A superfície de um cubo oco, de aresta , é feita de um material que se encolhe uniformemente a uma taxa constante de . Determine com que taxa está diminuindo o volume do cubo no momento em que sua aresta mede .
Ver solução completaQuestão 74
Determine os intervalos nos quais é crescente e nos quais é decrescente.
Ver solução completaQuestão 76
Determine os intervalos nos quais é crescente e nos quais é decrescente.
Ver solução completaQuestão 77
Calcule a derivada das seguintes funções, usando as regras de derivação:
Ver solução completaQuestão 78
Calcule os seguintes limites (Não é permitido o uso da regra de l´Hôspital):
b.
Ver solução completaQuestão 81
[Queda livre com resistência do ar.] Considere um objeto de massa m que é largado em queda livre numa situação em que a força de resistência que o ar oferece é diretamente proporcional à velocidade do objeto com constante de proporcionalidade k.
- Coloque a origem do eixo de coordenadas na posição inicial do objeto e com sentido positivo na direção do movimento. Use a segunda lei de Newton para concluir que .
- Mostre que essa situação pode ser descrita por encontrar uma função s(t) que satisfaz
- Mostre que, para quaisquer números A e B, a função satisfaz a equação .
- Mostre que, para satisfazer e , então .
- Mostre que .
Questão 82
Considere um sistema massa-mola sem atrito em que a massa do sistema é m e a constante de elasticidade da mola é .
- Coloque a origem do eixo de coordenadas na posição de repouso do sistema e use a segunda lei de Newton e a lei de Hooke para para concluir que
- Assuma posição inicial e velocidade inicial são e , respectivamente, e mostre que essa situação pode ser descrita por encontrar uma função que satisfaz
- Mostre que, para quaisquer números e , a função satisfaz , em que .
- Mostre que, para satisfazer e , então .
- Mostre que .
- Determine para e . Interprete o resultado fisicamente.
- Determine para e . Interprete o resultado fisicamente
Questão 83
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 84
 Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 87
Considere a função
Obtenha a equação da reta tangente à curva no ponto Em que ponto a reta tangente é paralela a
Ver solução completaQuestão 88
A quantidade de carga , em coulombs (C), que passa através de um ponto em um fio até o instante (medido em segundos) é dada por
Em que e são constantes. Determina a corrente neste ponto do fio no instante t. Quais são as unidades de medida?
Ver solução completaQuestão 95
- Calcular a derivada da função, onde ela existir, nos seguintes casos:
Ver solução completaQuestão 96
Calcular a derivada da função, onde ela existir, nos seguintes casos:
Questão 97
4. Resolva as seguintes questões.
- Mostre que a afirmação “qualquer função possui no máximo uma assíntota horizontal” é falsa, usando a função .
- Dada , , use a definição de derivada para mostrar que .
- Uma demonstração errada do item acima é a seguinte:
Seja , onde e , pela regra do produto, e como tem-se .
Encontre o erro na demonstração acima.
Ver solução completaQuestão 98
3. Usando as regras de derivação, calcule as derivadas das seguintes funções:
b)
Ver solução completaQuestão 101
Calcule (atenção: não é permitido usar derivadas no cálculo dos limites):
e)
Ver solução completaQuestão 107
11) Derive a função. (Se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 108
15) Derive a função. (Se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 109
12) Derive a função. (Se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 110
13) Derive a função. (Se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 115
Encontre a derivada das seguintes funções nos pontos dados
Para , encontre .
Ver solução completaQuestão 118
10. (1EE-2017.2-Adaptada) Calcule as derivadas das seguintes funções:
a)
Ver solução completaQuestão 119
10. (1EE-2017.2-Adaptada) Calcule as derivadas das seguintes funções:
c)
Ver solução completaQuestão 124
C8. Seja uma função diferenciável. Determine uma expressão para a derivada das funções abaixo.
a)
b)
c)
Ver solução completaQuestão 125
A quantidade de carga , em coulombs (C), que passa através de um ponto em um fio até o instante (medido em segundos) é dada por
Em que e são constantes. Determina a corrente neste ponto do fio no instante t. Quais são as unidades de medida?
Ver solução completaQuestão 140
Use o exercício anterior e a regra do quociente para determinar a derivada das funções
abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
(a)
Ver solução completaQuestão 144
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
d.
Ver solução completaQuestão 145
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
e.
Ver solução completaQuestão 146
Use o exercício anterior e a regra do quociente para determinar a derivada das funções
abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
(b)
Ver solução completaQuestão 147
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
b.
Ver solução completaQuestão 148
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
f.
Ver solução completaQuestão 149
2) Sejam , e três funções deriváveis definidas em tal que . Considere a função
Sabe-se que
E que , e .
O valor de é
Escolha uma:
a)
b)
c)
d)
e)
Ver solução completaQuestão 154
Considere a curva definida pela equação . Calcule e encontre uma equação da reta tangente à curva no ponto .
Ver solução completaQuestão 161
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 166
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 168
Calcule (atenção: não é permitido usar derivadas no cálculo dos limites):
d)
Ver solução completaQuestão 171
Nas videoaulas, você viu as primeiras regras de derivação (veja quadros abaixo com três possíveis escritas). Sejam u e v funções de x e c um número real.
Utilize essa tabela e a tabela da lista de exercícios 2.5 na resolução dos exercícios.
Determine a derivada das funções abaixo.
Ver solução completaQuestão 172
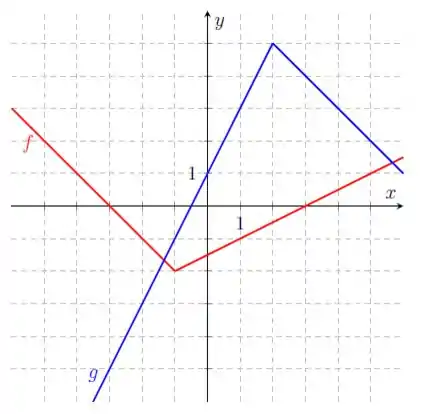
Q12. Considere , com uma função duas vezes diferenciável. Então, a função é duas vezes diferenciável e satisfaz.
Questão 175
Utilize a regra do produto ou do quociente para derivar as funções abaixo:
Ver solução completaQuestão 177
Considere a função e suas derivadas definidas abaixo
As assíntotas do gráfico de é correto afirmar que:
- são as únicas assíntotas verticais e não existem assíntotas horizontais
- são as únicas assíntotas verticais e é a única assíntota horizontal
- é a única assíntota vertical e é a única assíntota horizontal
- é a única assíntota vertical e não existem assíntotas horizontais
- não existem assíntotas verticais e é a única assíntota horizontal
Questão 180
Utilize a regra do produto ou do quociente para derivar as funções abaixo:
Ver solução completaQuestão 181
Utilize a regra do produto, regra do quociente e regra da cadeia para derivar as funções abaixo:
Ver solução completaQuestão 182
Utilize a regra do produto, regra do quociente e regra da cadeia para derivar as funções abaixo:
Ver solução completaQuestão 183
Utilize a regra do produto, regra do quociente e regra da cadeia para derivar as funções abaixo:
Ver solução completaQuestão 184
Utilize a regra do produto, regra do quociente e regra da cadeia para derivar as funções abaixo:
Ver solução completaQuestão 185
Utilize a regra do produto, regra do quociente e regra da cadeia para derivar as funções abaixo:
Ver solução completaQuestão 186
Considere a função e suas derivadas definidas abaixo
Sobre os pontos críticos e extremos relativos locais da função , podemos afirmar:
- o conjunto dos pontos críticos de é , possui máximo relativo em e não possui mínimo relativo
- o conjunto dos pontos críticos de é , possui mínimo relativo em e não possui máximo relativo
- o conjunto dos pontos críticos de é . possui máximo relativo em e não possui mínimo relativo
- o conjunto dos pontos críticos de é . possui mínimo relativo em e não possui máximo relativo
- não possui pontos críticos nem extremos relativos
Questão 192
5 - De uma folha de alumínio com de largura, deseja-se construir uma calha, dobrando-se os lados da folha para cima e formando duas abas de mesmo tamanho, de modo que estas abas façam o mesmo ângulo com a horizontal. Qual a largura das abas e que ângulo elas devem fazer com a horizontal para que a capacidade da calha seja máxima?
Ver solução completaQuestão 195
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
-
Ver solução completaQuestão 196
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
-
Ver solução completaQuestão 197
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
c.
Ver solução completaQuestão 198
- Use o exercício anterior e a regra do quociente para determinar a derivada das funções abaixo. Em seguida, determine as assíntotas verticais de cada uma delas.
-
Ver solução completaQuestão 200
Seja o único número real tal que a reta tangente ao gráfico de no ponto passa pelo ponto . Então o valor de vale quanto?
Ver solução completaQuestão 201
4) Para uma bola arremessada verticalmente sem resistência do ar, temos que a energia mecânica
Se conserva, onde e são, respectivamente, a posição e a velocidade instantâneas, é a massa do bloco e é a gravidade. Supondo que , e que , temos que é a solução da seguinte equação
Como ilustra os itens a seguir, a equação pode ser melhor entendida a partir do fato de que, se a derivada de uma função for identicamente nula em um intervalo, então a função é necessariamente constante.
a) Calcule as derivadas das funções e .
b) Lembrando que se uma função tem derivada identicamente nula em um intervalo , então ela é constante em , use o item anterior e as informações dadas para obter uma relação entre as funções e .
c) Use o item anterior e a condição inicial para obter a expressão de .
d) Determine a velocidade no instante .
Questão 202
5) Denote por a velocidade de um corpo de massa que foi lançado verticalmente com velocidade inicial e sujeito a uma força de resistência do ar . Nesse caso, usando a aproximação da aceleração da gravidade, pode-se mostrar que é solução do problema de valor inicial
Para encontrar a solução , resolva os itens seguintes.
a) Calcule as derivadas das funções e .
b) Lembrando que se uma função tem derivada identicamente nula em um intervalo , então ela é constante em , use o item anterior e as informações dadas para obter uma relação entre as funções e .
c) Use o item anterior e a condição inicial para obter a expressão de .
d) Determine o instante em que o corpo alcança a altura máxima.
Ver solução completaQuestão 218
Considere a função e suas derivadas definidas abaixo
- Determine os intervalos onde o gráfico de é côncavo para cima e os intervalos onde o gráfico de é côncavo para baixo.
- Determine, se existirem, o(s) ponto(s) de inflexão do gráfico de .
- Esboce o gráfico de
Questão 224
Sejam funções deriváveis.
- Use a regra do produto para provar que:
- Diferencie
Questão 227
Encontre a derivada das funções abaixo de duas formas (aplicando diretamente uma regra ou simplificando/multiplicando primeiro e aplicando outra regra) e verifique que o resultado é o mesmo
Ver solução completaQuestão 229
2. Assuma que e sejam funções diferenciáveis em e defina para todo . Sabendo que , , e , calcule .
Ver solução completaQuestão 230
Utilizando as regras de derivação, calcule a derivada das seguintes funções:
c)
Ver solução completaQuestão 231
Utilizando as regras de derivação, calcule a derivada das seguintes funções:
d)
Ver solução completaQuestão 237
O movimento de uma mola sujeita a uma força de atrito é frequentemente modelado pelo produto de uma função exponencial e uma função seno. Suponha que a equação do movimento de um ponto sobre essa mole é:
em que s é medida em centímetros e t em segundos.
Encontre a velocidade após t segundos.
Ver solução completaQuestão 238
C5. Uma das regras de derivação é a regra do produto, que diz que
- Aplique a fórmula acima duas vezes em sequência e encontre uma regra para derivada do produto de três funções.
- Estenda seu raciocínio para encontrar uma fórmula para a derivada do produto de funções.
- Utilize a fórmula descoberta para calcular a derivada de .
Questão 244
9. Determine a derivada da função em cada caso.
a) Utilizando a definição de derivada.
b) Utilizando regras de derivação.
Ver solução completaQuestão 247
Dizemos que é uma raiz dupla de uma função polinomial f se , para alguma outra função polinomial .
a. Mostre que é raiz dupla de f se e somente se é raiz tanto de f quanto de f ′.
b. Quando tem raiz dupla? Interprete geometricamente.
Ver solução completaQuestão 253
Utilize a regra do produto ou do quociente para derivar as funções abaixo:
Ver solução completa