Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 37
Um copo de papel em forma de cone deve conter de água. Encontre a altura e o raio do copo que requer a menor quantidade de papel.
Passo 1
Então pessoal, como estamos falando de um copo de papel em forma de cone, temos que a representação do copo seria:
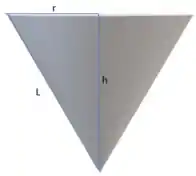
E assim como já indicado na figura, vamos chamar o raio de , a altura de e a altura inclinada de , tudo bem? Show! O volume do cone é dado pela seguinte equação:
A área do setor circular do cone é:
Ok, vamos guardar essas informações!
Passo 2
Isolando da primeira equação, teremos:
Pelo teorema de Pitágoras podemos fazer:
Substituindo na equação da área do setor circular do cone:
Note que estamos estabelecendo uma expressão para a área porque é isso que nos importa, não o volume do cone. O problema aqui se baseia em quantidade de papel, isso tem que ficar claro, tudo bem?
A fim de facilitar nossa vida, vamos elevar os dois membros da equação ao quadrado, se liga:
Ademais, vamos fazer:
Então:
Isso aqui é só para facilitar nossa derivação, galera!
Passo 3
Como estamos falando de minimização na quantidade de papel, estamos falando de ponto de mínimo, não é mesmo? Logo, derivando nossa expressão:
Igualando a zero:
Passo 4
Agora que encontramos , para encontrarmos é bem tranquilo, basta substituirmos o valor de encontrado na expressão de , saca só:
Simplificando um pouco:
E essas são as dimensões necessárias para minimizar a quantidade de papel do copo, galera! 😉