Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 26
a) Encontre uma aproximação para a integral usando uma soma de Riemann com as extremidades direitas e .
b) Faça um diagrama como a Figura 3 para ilustrar a aproximação da parte (a).
c) Use o Teorema 4 para calcular .
d) Interprete a integral da parte (c) como uma diferença de áreas e ilustre com diagramas como o da Figura 4.
Passo 1
Opa! E aí, bora resolver essa questão?!
No item a) o enunciado pede pra a gente calcular a soma de Riemann para essa função aqui:
No intervalo . Ou seja, queremos calcular:
O próprio enunciado já diz que a gente deve resolver o problema pela soma de Riemann, pra isso a gente vai usar essa forma geral aqui:
A soma de Riemann para aproximar uma integral de uma função definida no intervalo é dada da seguinte forma:
Em que
e
Onde é o número de subintervalos e é a largura do subintervalo.
No item b) teremos que fazer um diagrama para ilustrar a aproximação da parte (a).
No item c) usaremos o Teorema 4 para calcular .
E no item d) devemos interpretar a integral da parte (c) como uma diferença de áreas e ilustrar com diagramas como o da Figura 4.
Bora lá!! 😉
Passo 2
Na letra a) queremos encontrar uma aproximação para a integral usando uma soma de Riemann com as extremidades direitas e .
Para isso, devemos saber que a soma de Riemann é um método matemático usado para aproximar a integral de uma função definida em um intervalo específico.
Onde é dado por:
Como a gente vai pegar os pontos da extremidade direita de cada intervalo, para achar cada ponto fazemos:
Pro nosso caso teremos:
Na prática, pra fazer o exercício, vamos abrir a integral ali de cima e vamos ficar com:
Calculando cada uma das funções, teremos:
Assim, a soma se torna:
Passo 3
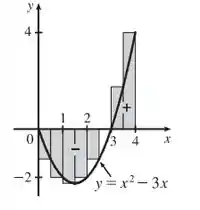
Na letra b) queremos fazer um diagrama como a Figura 3 para ilustrar a aproximação do que acabamos de calcular.
Lembrando que a Figura 3 é essa:
Assim, plotando a figura e aplicando os subintervalos, temos:
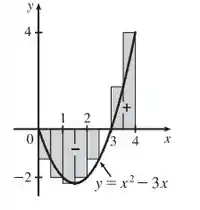
Passo 4
Na letra c) queremos usar o Teorema 4 para calcular a nossa integral.
Mas o que diz o Teorema 4???
Bom... O teorema 4 diz que se for integrável em , então
Onde e
Agora bora aplicar!! 😉
Passo 5
Aplicando o Teorema 4, temos:
Passo 6
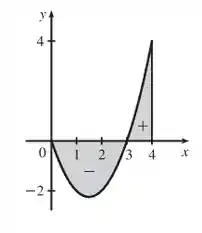
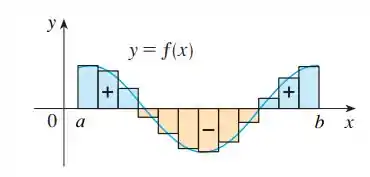
Por fim, na letra d) queremos interpretar a integral da letra c) como uma diferença de áreas e ilustre com diagramas como o da Figura 4.
Lembrando que a Figura 4 é essa:
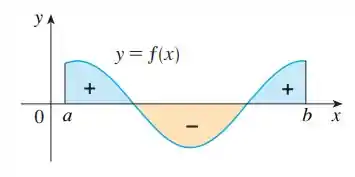
Bom... vamos lá.
Nesse sentido, temos que:
Onde é a área positiva, e , a negativa.
Assim, temos:
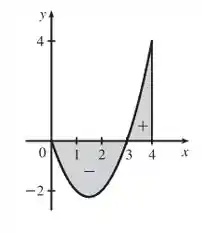
Entendeu direitinho?? Responde aee 😉
Resposta
