Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 7.7 - Ex. 34

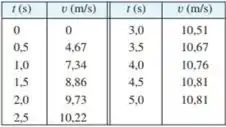
Um radar móvel foi usado para monitorar a velocidade de um corredor durante os primeiros 5 segundos de uma corrida (veja a tabela). Use a regra de Simpson para estimar a distância que o corredor correu durante esses 5 segundos.

Passo 1

Fala aí, pessoal! 😬

Nesse problema queremos obter a distância percorrida por um corredor a partir dos dados fornecidos pela tabela do enunciado usando a regra de Simpson.

Tem ideia de como fazemos isso? 👀

Antes de começar o exercício, vamos determinar qual será o tamanho do intervalo em análise:

Δ t = 5 - 0 10 → Δ t = 0,5

Vamos começar o exercício relembrando rapidamente a fórmula para aproximar o valor de uma integral pela fórmula de Simpson:

∫ a b f x d x ≅ S n = Δ x 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + … + 2 f x n - 2 + 4 f x n - 1 + f x n

Onde nós temos:

Δ x = b - a n ,     x i = a + i Δ x

Sacou? Bora começar! 😊

Passo 2

Então, subsituindo os valores na fórmula, temos:

S 6 = 0,5 3 f 0 + 4 f 0,5 + 2 f 1 + 4 f 1,5 + 2 f 2 + 4 f 2,5 + 2 f 3 + 4 f 3,5 + 2 f 4 + 4 f 4,5 + f ( 5 )

Substituindo os valores fornecidos na tabela do enunciado, temos:

S 6 = 0,5 3 0 + 4 4,67 + 2 7,34 + 4 8,86 + 2 9,73 + 4 10,22 + 2 10,51 + 4 10,67 + 2 10,76 + 4 10,81 + 10,81

Dessa forma, o resultado será:

S 6 = 44,735   m

E aí! o que achou? Responde Aí! 😁

Resposta

S 6 = 44,735   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

b) Encontre novas estimativas usando 8 retângulos.
Lendo os valores do gráfico dado de f , utilize quatro retângulos para encontrar as estimativas inferior e superior para a área sob o gráfico dado de f de x = 0 ate x = 8 . Em cada caso, esboce os ret
a) Faça o gráfico da função f x = x - 2 ln ⁡ x,1 ≤ x ≤ 5 b) Estime a área sob o gráfico de f usando quatro retângulos aproximantes e tomando como pontos amostrais ( i ) as extremidades direitas e ( i
Avalie as somas superiores e inferiores para f x = x 2 + 1 , - 1 ≤ x ≤ 1, com n = 3 e 4. Ilustre com diagramas como Figura 14.
Avalie as somas superiores e inferiores para f x = 2 + s e n x ,0 ≤ x ≤ π , com n = 2 ,4 e 8 . Ilustre com diagramas como na figura 14.