Calcule as aproximações , , e para e . Então calcule os erros correspondentes , , e . (Arredonde seus resultados para seis casas decimais. Você pode usar o comando soma em um sistema algébrico computacional.) Quais observações você pode fazer? Em particular, o que acontece aos erros quando é dobrado?
Passo 1
Vamos começar calculando a integral normalmente:
E agora vamos usar as fórmulas para cada uma das aproximações no nosso intervalo de comprimento .
Passo 2
Primeiro vamos usar , nesse caso, cada um dos intervalos será:
Na aproximação pelo extremo esquerdo, analisamos os pontos no extremo esquerdo de cada intevalo. Em outras palavras, começamos no zero e vamos somando :
Na aproximação pelo extremo direito, começamos com e vamos somando :
Na aproximação pelo ponto médio, começamos em , e vamos somando :
Na aproximação trapezoidal, colocamos pesos nos termos do meio, e dividimos tudo por dois. Em seguida vamos desde o início até o fim do intervalo em passos de :
E agora para calcular o erro de cada um, é só fazer a diferença até o valor real que calculamos no primeiro passo:
Passo 3
Agiora vamos fazer praticamente a mesma coisa para . Como o enunciado diz que podemos usar um computador, vamos apenas deixar as fórmulas indicadas aqui:
E agora é só calcular o erro, conforme fizemos antes:
Passo 4
Por fim, vamos fazer :
E agora é só calcular o erro, conforme fizemos antes:
Passo 5
Que observações podemos fazer sobre os erros?
Em primeiro lugar, e sempre deram resultados negativos, isso indica que e tendem a superestimar a integral.
Por outro lado, e sempre são negativos, indicando que e tendem a subestimar a integral.
Em segundo lugar, fica claro que os valores dos erros diminume conforme o valor de aumenta.
Em terceiro lugar, os erros de e são sempre bem menores que os demais.
E quando é dobrado, os erros de e caem aproximadamente pela metade, e os erros de e caem aproximadamente por um fator :
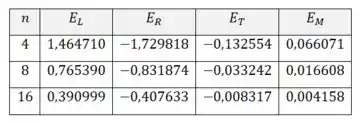
Resposta
Valores podem ser calculados computacionalmente (ver tabela). Conforme é dobrado, os erros e caem aproximadamente pela metade, e os erros caem aproximadamente por um fator .