Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 43

Encontre a área que está acima do e i x o   x mas abaixo da curva y = ( 1 - x ) ( x - 2 ) . Faça um esboço dessa região.

Passo 1

Queremos encontrar uma região que está acima do e i x o   x e abaixo da curva especificada. A curva dada cruza o e i x o   x nos pontos:

x = 1

E

x = 2

Pois são as raízes da curva em 1,0 e 2,0 .

Multiplicando os termos e simplificando a função:

y = ( 1 - x ) ( x - 2 )

y = - x 2 + 2 x - 2

A área requerida será a integral dessa curva, e será definida pelos pontos [1, 2] onde a função cruza o eixo.

Passo 2

Integrando a função dada:

A = ∫ 1 2 - x 2 + 3 x - 2 d x

A = - x 3 3 + 3 x 2 2 - 2 x 1 2

Aplicando o valor encontrado, nos limites de integração :

A = - 2 3 3 + 3.2 2 2 - 2.2 - - 1 3 3 + 3.1 2 2 - 1.2

A = - 8 3 + 6 - 4 - - 1 3 + 3 2 - 2 = - 2 3 + 5 6

A = 1 6

Passo 3

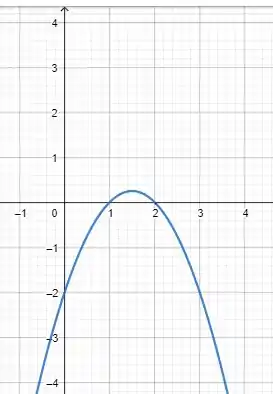
Esboçando a curva, teremos algo com essa aparência :

Resposta

A = 1 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área entre a curva y = 2 1 - x e o intervalo - 1 ≤ x ≤ 1 do eixo x .
Determine a área das regiões compreendidas entre x = 3 s e n y c o sy e x = 0 ,0 ≤ y ≤ π 2
Determine a área da região entre a curva y = 3 - x 2 e a reta y = - 1 . Em relação a y
Determine a área das regiões compreendidas entre y = s e c π x 3 2 e y = x 1 3 , - 1 ≤ x ≤ 1
Determine a área entre a curva y = t g x e o eixo x de x = - π 4 até x = π 3 .