Encontre a área da região delimitada pela hipérbole e a reta

Esse tipo de questão depende um pouco da visualização do gráfico, pra isso vamos entender um pouco melhor da hipérbole. Sua forma geral é assim:

Podemos manipular a nossa equação pra descobrirmos e :

Temos então uma hipérbole horizontal com e . Um gráfico geral pra esse tipo de hipérbole tem essa carinha aqui:

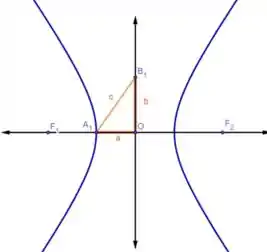
Repara que é a distancia entre o até o vértice da hipérbole. Como queremos a área da região delimitada pela hipérbole e a reta , então podemos ignorar o lado esquerdo do gráfico.

Podemos fazer um esboço beeem simples, sem tabelinha nem nada:

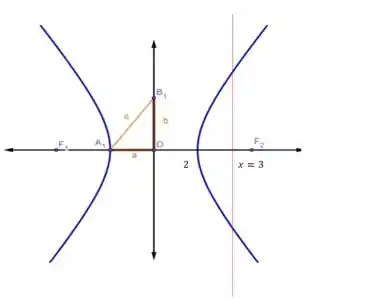
Agora vamos pensar em um plano de ação! Conseguimos perceber duas coisas:

1. Os limites de integração serão e ;
2. A hipérbole é simétrica em relação ao eixo , então podemos calcular a área acima do eixo , por exemplo, e multiplica-la por .

Vamos isolar o na equação da hipérbole:

Podemos escrever então:

Jogamos a constante pra fora:

Vamos resolver esta integral pela substituição trigonométrica, pra isso, vamos dizer o seguinte. Seja:

Calculando os novos limites de integração :

Substituindo na integral, ficamos com:

Pra resolver esta integral, precisamos lembrar da seguinte propriedade trigonométrica: :

Para a integral , temos uma integração por partes:

Diremos que

Passando o termo para o lado esquerdo da igualdade:

É tabelado que:

Agora podemos voltar para a nossa integral original: