Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 36
Calcule a integral
Coloque em um gráfico o integrando e a integral indefinida e verifique se sua resposta é razoável.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular a integral indefinida da função e esboçar essa função junto com o resultado da integral em um gráfico.
Para calcular a integral, vamos usar uma substituição trigonométrica, para tentar fugir dessa raiz no denominador. Assim, vamos fazer:
Diferenciando, temos que:
Substituindo isso na nossa integral, vamos calcular. Então, vamos lá!
Passo 2
Substituindo na nossa integral, ficamos com:
Colocando em evidência na raiz:
Agora a gente precisa lembrar da seguinte propriedade trigonométrica: . Então, temos:
Agora podemos eliminar a raiz, simplificando ela com o termo ao quadrado:
E simplificando numerador e denominador, temos:
Agora como temos a identidade trigonométrica , podemos escrever:
Passo 3
Beleza, fugimos da raiz, agora vamos resolver essa integral pelo método da substituição. Assim, seja:
Temos que:
Substituindo na integral:
E integrando, temos:
Onde é uma constante de integração.
Agora vamos voltar pra nossa variável , usando . Assim, teremos:
Passo 4
Mas lá no passo , definimos . A partir disso, temos:
Logo:
Porém, precisamos encontrar uma expressão para . Na resolução da integral, vimos que:
Então, temos:
E
Passo 5
Agora, só falta substituirmos tudo no resultado. Assim:
Passo 6
E o nosso gráfico de e , será:
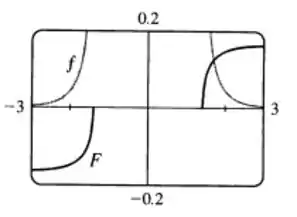
Pelo gráfico, podemos ver que a resposta obtida é razoável.
Valeu, galera! Até a próxima! 😉