Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 34
Encontre a área da região que está dentro de ambas as curvas
Passo 1
Olá, meu amigo. Vamos resolver essa atividade sobre área de curvas parametrizadas.
Temos duas curvas:
E queremos encontrar a área da região que está simultaneamente entre as duas curvas. Vamos dar uma olhada em que tipo essas curvas são, transformando-as em coordenadas cartesianas.
Sabe-se que a as coordenadas polares e cartesianas se relacionam com:
Então para a primeira figura:
E a equação:
Se torna:
Vamos utilizar a relação:
Que é a equação de uma circunferência simétrica em . Se fizermos a mesma análise de
Vamos encontrar uma circunferência simétrica em .
Vamos plotar as curvas para termos ideia da área que a gente tá calculando.
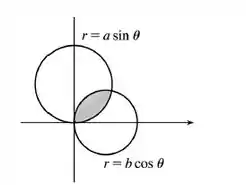
Portanto, queremos a área dessa região sombreada.
A área de uma curva em coordenadas polares é dada por
Então temos que identificar cada termo dessa integral aí, substituir e calcular.
Para encontrar esse intervalo, no caso dessa questão, vamos precisar encontrar os pontos de interseção das duas curvas, já que queremos a área dentro de ambas as curvas.
Passo 2
Para isso, basta igualarmos as duas curvas:
Eu sei que parece estranho, mas é a mesma coisa que estávamos fazendo até agora. Acontece que nessa questão o nosso não tem um valor especfico, não é um ângulo “palpável” digamos assim, é uma parada que tá em função de dois parâmetros.
Mas a ideia é exatamente a mesma! Pense no como um ângulo qualquer!
Agora vamos pensar. Se a gente imaginar uma reta bem no ponto de interseção entre as duas curvas, é como se nossa região sombreada fosse a curva de até e depois passasse a ser a curva , de até .
Vê se você consegue visualizar isso:
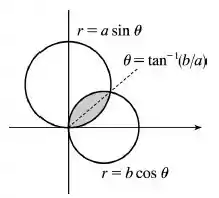
Então, teremos dois intervalos de integração:
E
DICA: Essa questão é igual a questão , só que lá a gente tinha .
Passo 3
Continuando, falta a gente descobrir quem é o .
O é a própria parametrização.
Assim, como temos duas curvas, vamos ter dois (e duas integrais, afinal, até definimos dois intervalos de integração ali no passo 2).
Então agora é só substituir e integrar esse negócio.
Passo 4
Vamos lá:
Para não ficar carregando essa coisa gigante o tempo todo na nossa integral, vou escrever , tá bem?
Realizando os quadrados:
Utilizando de identidades trigonométricas:
Retirando a constante da integral:
Agora a gente pode resolver essas integrais:
Colocando os limites de integração:
Colocando os valores dos senos:
Escrevendo :
Como:
Assim substituindo a relação:
Realizando o produto no segundo termo:
Agora colocando de volta o arco tangente: