Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 43
Os pontos de intersecção da cardioide
E do laço espiral
Não podem ser encontrados exatamente. Use uma ferramenta gráfica para encontrar os valores aproximados de nos quais eles se interceptal. Então, use esses valores para estimar a área que está dentro de ambas as curvas.
Passo 1
A área de uma curva em coordenadas polares é dada por
Plotando as duas curvas com a ajuda de uma ferramenta gráfica, temos
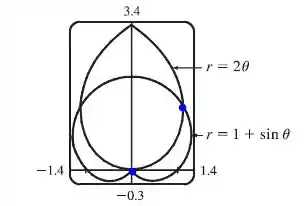
Com isso, vemos que as curvas se intersectam em dois pontos, que foram esses que eu marquei de azul aí.
Um deles é a origem, ou seja, .
O outro a gente consegue descobrir dando um zoom na ferramenta.
Com isso, vemos que temos o ângulo
Show de bola, encontramos nossos valores de de interseção das curvas.
Passo 2
Agora vamos ao cálculo da área.
Mas, para isso, vamos antes entender que área que vamos calcular.
Queremos a área entre as duas curvas, portanto, queremos essa área pontilhada ai:
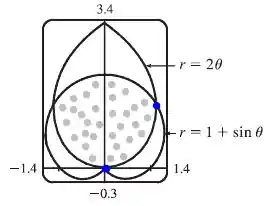
Mas, se você reparar, nossa figura é simétrica, então dá pra dividir essa área em dois e calcular só metade dela e depois multiplicar por dois, certo?
Passo 3
Ok, agora vamos pensar o intervalo de integração e ao valores de .
Podemos dizer que nossa região de interesse, que é a região pontilhada (vamos considerar só a parte que tá no primeiro quadrante, tá bem? Já que depois a gente vai multiplicar por 2 mesmo...)
Isso vai facilitar o nosso intervalo de integração, porque estaremos no primeiro quadrante, e consequentemente, vai tornar a integral menos pior.
Podemos dizer que nossa região é formada pela curva
De
Até
E pela curva
De
Até
Concorda?
Show, então esses são nossos e nossos intervalos de integração.
Passo 4
As integrais ficam:
Assim, a área total é