Encontre a área da região que está dentro de ambas as curvas
Passo 1
Olá, meu amigo. Tudo bem com você?!
Vou te ajudar a resolver essa atividade hoje.
Temos as curvas em coordenadas polares:
E queremos calcular a área da região que está dentro das duas figuras simultaneamente.
Temos aqui duas limaçons, do tipo:
A primeira equação é de uma figura simétrica em relação ao eixo polar e a segunda é uma figura simétrica em relação ao eixo a . Se não temos laços no nosso limaçon, e se o sinal for positivo então elas estão no sentido positivo do eixo ordenado.
Vamos plotar as curvas para termos ideia da área que a gente tá calculando.
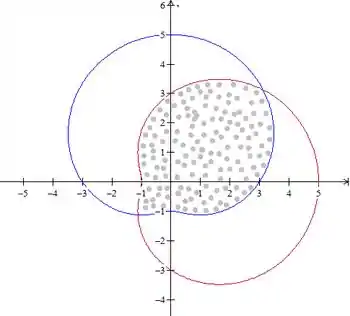
Portanto, queremos a área dessa região sombreada.
A área de uma curva em coordenadas polares é dada por:
Então temos que identificar cada termo dessa integral aí, substituir e calcular.
Para encontrar esse intervalo, no caso dessa questão, vamos precisar encontrar os pontos de interseção das duas curvas, já que queremos a área dentro de ambas as curvas.
Passo 2
Vamos igualar as curvas para encontrar os seus limites de integração:
Então vamos pensar.
Se a gente imaginar uma reta bem no ponto de interseção entre as duas curvas, é como se nossa região pontilhada fosse a curva vermelha, que é a curva de até e depois passasse a ser a curva vermelha, , de até .
Vê se você consegue visualizar isso:
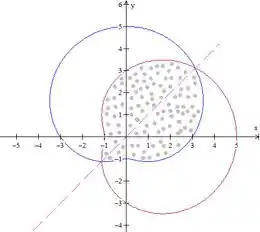
Daí, com isso, estamos dividindo nossa área em duas partes e só vamos calcular metade dela. Depois é só multiplicar por , já que a figura é simétrica, beleza?
Passo 3
Continuando, falta a gente descobrir quem é o .
O é a própria parametrização.
Mas agora a gente precisa ficar esperto. Como dividimos nossa curva em partes e só vamos calcular a integral de até , temos que nos atentar, como a gente tinha conversado ali em cima, que nesse intervalo a nossa região de interesse é definida apenas pela curva vermelha, que é a curva:
Assim, esse é o nosso .
Então agora é só substituir e integrar esse negócio.
Passo 4
Vamos lá:
Substituindo:
Realizando o produto notável:
Reescrevendo utilizando a identidade trigonométrica
Simplificando:
Integrando cada um dos termos:
Aplicando os limites de integração:
Assim, a área total da nossa regi��o é: