Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 5
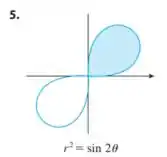
Encontre a área da região sombreada:
Passo 1
Eaee, belezinha?? Bom... queremos determinar a área sombreada da seguinte figura:
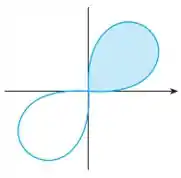
Onde a equação dessa curva é dada por:
Para isso, sabemos que a área de uma curva polar é dada por:
Assim, precisamos determinar o intervalo de em que essa região está para podermos determinar os limites de integração na equação da área.
Passo 2
Bom... perceba que a região sombreada se encontra no primeiro quadrante inteiro, ou seja, , pela equação da área:
Substituindo :
Passo 3
Para resolvermos a integral, vamos primeiro calcular a indefinida e no final a gente substitui os limites:
Colocando a constante para fora:
Resolvendo a integral pela Regra da Cadeia, obtemos:
Substituindo os limites:
Resposta
Exercícios de Livros Relacionados
Encontre a área da região que está dentro da primeira curva e fora da segunda curva.26. r = 1 + c o s θ , r = 2 - c o s θ
Encontre todos os pontos de inserção das curvas dadas.38. r = 1 + c o s θ , r = 1 - s e n θ
Encontre a área da região sombreada:
Encontre a área da região sombreada:
Esboce a curva e encontre a área que ela encerra: r = 2 - c o s θ