Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação polar:
Queremos esboçar essa curva polar.
Mas, para isso, temos que esboçar primeiro a curva nas coordenadas cartesianas.
Mas por que isso?
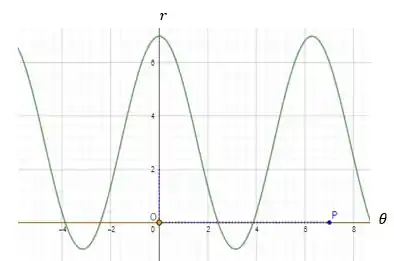
Veja... quando a gente plota em coordenadas cartesianas, fica melhor para observarmos onde a curva está com um pico mais alto (que é o tamanho de ) de acordo com o seu ângulo .
Assim, afica mais fácil de desenhar a nossa curva!!
Se ainda não entendeu, continua aqui que vc vai entender direitinho 😉
Passo 2
Vamos analisar a nossa equação:
A gente conhece a curva do cosseno:
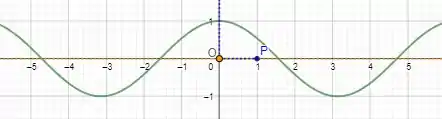
Obs: não ligue para o ponto . O ponto serve apenas para indicar o centro.
Perceba que a única diferença entre essa curva e a curva é que tem um somando (que indica que a curva está deslocada em unidades para cima) e um multiplicando o cosseno (que indica que a amplitude foi multiplicada por ).
Assim, temos que a nossa curva em coordenadas cartesianas é dada por:
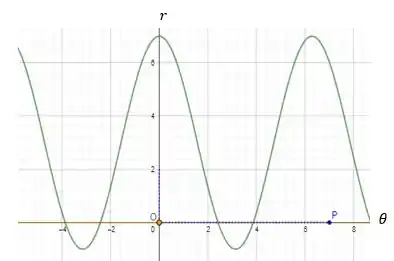
Agora vamos plotar a nossa curva polar!!
Passo 3
Vamos analisar primeiro o intervalo de a (primeiro quadrante).
Vemos que, nesse intervalo, o gráfico começa com e termina com . Assim, temos:
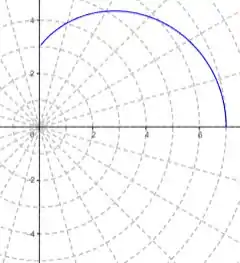
Agora, para o intervalo a , vemos que o gráfico começa com e assume valores negativos, terminando em .
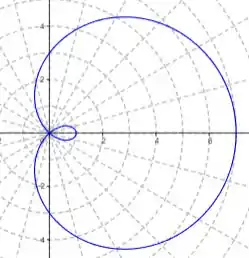
Isso indica que o gráfico faz um “nó” em outro quadrante, veja:
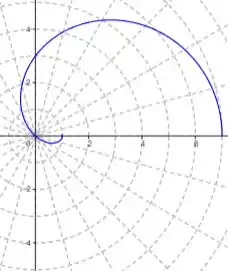
Obs: não existe negativo nesse gráfico. Esse negativo é só para indicar que ele “sai” do quadrante que estamos analisando.
Agora, a gente finaliza o intervalo de para pois o gráfico apresenta o mesmo comportamento, só que primeiro ele começa do nó e termina no ponto inicial:
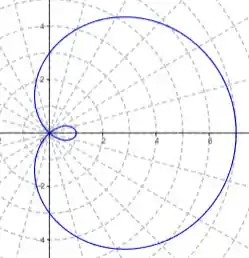
Logo, nota-se que a nossa figura é um cardióide!! 😉
Resposta