Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.3 - Ex. 34

Determine se o conjunto dado é ou não: (a) aberto, (b) conexo por caminhos e (c) simplesmente conexo.

Passo 1

Olá, tudo bem?

Vamos ver o que a questão está querendo.

Ela quer que a gente diga se a região que possui todos os pontos, menos o ponto é aberta, conexa por caminhos ou simplesmente conexa.

Sendo que uma região aberta, é uma região onde nunca conseguiremos sair. Normalmente isso ocorre quando temos uma descontinuidade, que é quando os extremos não estão incluídos ou algum ponto está faltando.

Uma região conexa por caminhos, é uma região em que podemos ir para qualquer lugar, sem sair dela.

Exemplo de uma região conexa por caminhos:

Exemplo de uma região não conexa por caminhos:

E simplesmente conexa, é uma região que podemos ir para qualquer lugar sem nenhuma restrição de caminho e sem sair dela. Ou seja, uma região sem ‘’buracos’’.

Exemplo de uma região simplesmente conexa:

Exemplo de uma região não simplesmente conexa:

Primeiro faremos um desenho da região

e depois veremos se ela se encaixa em cada uma das alternativas.

Ok?

Passo 2

Vamos fazer um desenho para ter uma ideia melhor da região que queremos analisar. E como vimos no passo 1, essa região são todos os pontos, menos o ponto .

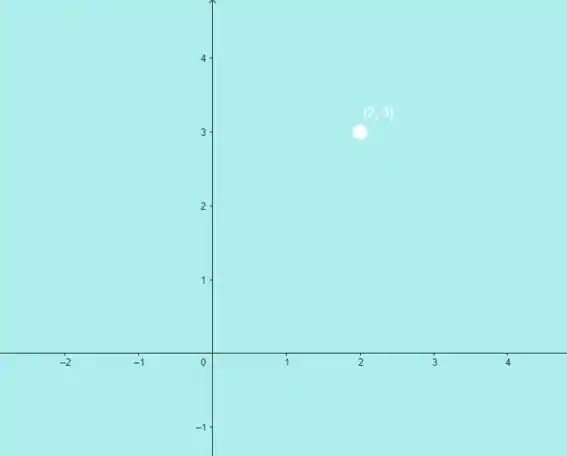
Então, a nossa região é toda essa área azul!

Passo 3

Na letra a, queremos saber se a região é aberta.

Vamos nos imaginar dentro dela.

Se quisermos sair da região, o único lugar para onde poderíamos ir, seria o ponto que não está dentro dela, conforme vamos andando, vamos chegando cada vez mais perto, porém, nunca pisaremos nele, pois