Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 31
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de em coordenadas cartesianas.
Passo 1
Vamos simplificar a equação dada?
Sabemos que:
Então:
Substituindo os intervalor la equaão e encontrar os valores de .
Para
Para
Sendo assim, r alcança seu valor máximo em 4 e o mínimo em 0. E esboçando o gráfico de r como função de em coordenadas cartesianas, temos:
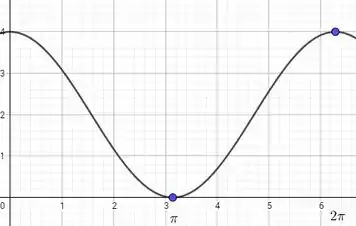
Passo 2
Agora só falta analisarmos a equação em coordenadas cartesianas. Esta curva será uma forma semelhante a uma pétala de rosa, simétrica em relação ao eixo e ao eixo .
- Os pontos mais distantes da origem na vertical ocorrem em e .
- Os pontos mais distantes da origem na horizontal ocorrem em devido à característica da função em coordenadas cartesianas. Quando , o termo atinge seu valor mínimo, resultando em .
Por outro lado, quando , o termo atinge seu valor máximo, resultando em .
- Esse gráfico terá uma forma de "petalas de rosa" se estendendo para fora da origem com pétalas e raio variando entre e .
Essa curva, em coordenadas polares, representa a seguinte cardioide:
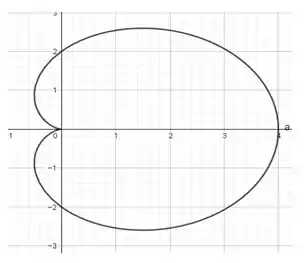
Resposta
A equação polar descreve uma espiral com duas pétalas que se afasta da origem à medida que aumenta. Em coordenadas cartesianas, essa curva assume a forma de uma "rosácea", simétrica em relação aos eixos e , com pontos mais distantes da origem ocorrendo em .
Eai gostou? Até a próxima!