Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 43
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de r como função de em coordenadas cartesianas.
Passo 1
Vamos começar a analisar a equação polar.
- A partir da estrutura da equação, temos que a amplitude A da função seno é , e a amplitude da constante é .
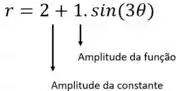
então a amplitude total é .
Isso significa que a curva oscilará entre (quando ) e (quando ).
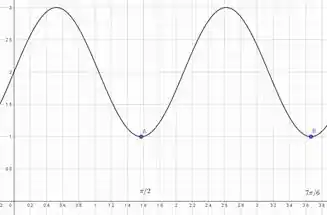
- Em termos do gráfico, o termo na equação polar indica que a curva começa a uma distância de 2 uniddes da origem ao longo do eixo radial.
Passo 2
Vamos analisar mais um pouco?
- A frequência é determinada pelo argumento do seno, que é , indicando três oscilações completas ao longo de um volta completa ().
- A função gerou uma curva espiralada devido à presença da função seno no termo . A oscilação periódica de com faz com que a curva se envolva em torno da origem, criando um padrão espiralado.
- O termo desloca a curva verticalmente, fazendo com que ela comece a uma distância de unidades da origem ao longo do eixo radial.
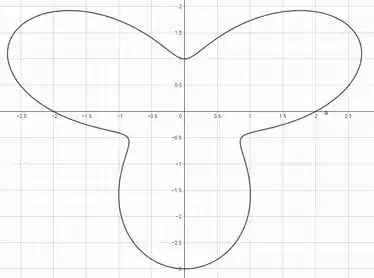
Essa curva representa a seguinte rosácea:
Resposta
O Bizu dessa questão é olhar para o argumento do seno, como temos a rosácea terá pétalas. Isso ocorre porque a função seno completa três ciclos completos (voltas) no intervalo de a , produzindo assim "subpétalas" ao longo de uma volta completa.
Sacou?
Sendo assim a rosácea resultante terá pétalas distintas em torno da origem.
Até a próxima questão!