Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 1
Encontre a área da região sombreada.
Passo 1
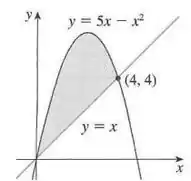
Opa, bora resolver esse problema! O enunciado nos dá o seguinte gráfico:
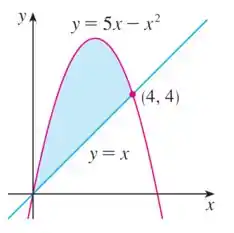
E pede para acharmos a área da região sombreada!
É importante lembrar que a área entre as curvas é dada pela integral da função que está em cima menos a função que está em baixo. Ou seja:
Os limites de integração serão e pois este é intervalo no eixo que delimita a região!!!
Passo 2
Assim, a área pedida será
Integrando:
Aplicando os limites de integração:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Calcule a área da região limitada pela curva dada(coordenadas polares). c ) ρ = cos 2 θ
Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares c )ρ = 1 eρ = 2 1 - cos θ
Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares c )ρ = 3 eρ = 2 1 - cos θ
Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares e )ρ = cos θeρ = sin θ
Calcule a área da intersecção da região limitada pelas curvas dadas em coordenadas polares a )ρ = 2 - cos θeρ = 1 + cos θ