Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 4f

Calcule a área da intersecção das região limitada pelas curvas dadas em coordenadas polares

c )   ρ = 1     e   ρ = 2 1 - cos ⁡ θ

Passo 1

Primeiro devemos achar os pontos de intersecção das funções:

1 = 2 1 - cos ⁡ θ → 1 2 = 1 - cos ⁡ θ → cos ⁡ θ = 1 - 1 2 = 1 2 → θ = cos - 1 ⁡ 1 2

Nesse caso vemos que dentro do intervalo 0 ,   2 π teremos dois valores ideais para esse θ que vai ser π 3   e 5 π 3 , a imagem vai ficar algo assim:

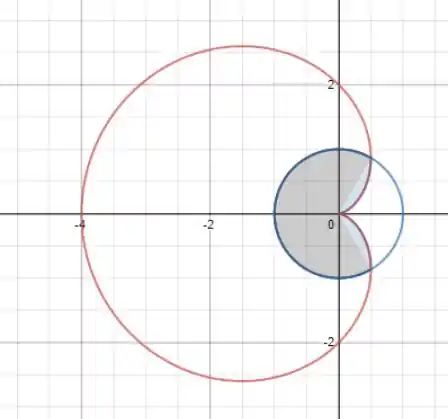
Queremos a área em comum entre as duas equações e pra isso temos que calcular a área delas porém não faz sentido calcular duas vezes, se não estamos calculando em excesso.

Pra que funcione bem vamos pegar uma área que vem de uma delas num dado intervalo somado com a área da outra função no resto do intervalo.

Como vimos no desenho, as intersecções vão rolar durante o intervalo π 3 , 5 π 3 , porém olhando pro gráfico, vemos que é mais fácil calcular a área da função   ρ = 1 no intervalo π 3 , 5 π 3 e que é mais fácil calcular a área de ρ = 2 1 - cos ⁡ θ no intervalo 5 π 3 , π 3 . Assim, vamos calcular as áreas.

Dá pra notar que ambas curvas tem área simétrica em relação ao semi eixo Ox, assim, vamos calcular o dobro da área em relação a metade do intervalo.

Passo 2

Daí calculamos cada área:

Á r e a   1 = 1 2 ∫ α β ρ 2 d θ = 1 2 ∫ 2 π 3 π 3 4 1 - cos ⁡ θ 2 d θ = 4 ∫ 0 π 3 1 - cos ⁡ θ 2

E

Á r e a   2 = 1 2 ∫ α β ρ 2 d θ = 1 2 ∫ π 2 2 π 3 1 2 d θ = ∫ π 3 2 π 3 1 d θ

Agora vamos calcular cada área e depois somamos:

Á r e a   1 = 4 ∫ 0 π 3 1 - cos ⁡ θ 2 d θ = 4 ∫ 0 π 3 1 - 2 cos ⁡ θ + cos 2 ⁡ θ d θ

4 ∫ 0 π 3 1 d θ - 8 ∫ 0 π 3 cos ⁡ θ d θ + 4 ∫ 0 π 3 cos 2 ⁡ θ =

Faremos a substituição: sin 2 ⁡ θ = 1 2 ( 1 - cos ⁡ 2 θ )

4 π 3 - 8 sin ⁡ θ π 3 0 + 4 ∫ 0 π 3 1 2 1 + cos ⁡ 2 θ d θ = 4 π 3 - 8 3 2 + 2 ∫ 0 2 π 3 1 + cos ⁡ 2 θ d θ =

e em seguida u = 2 θ → d u = 2 d θ

4 π 3 - 8 3 2 + 2 ∫ 0 π 3 1 + cos ⁡ 2 θ d θ = 4 π 3 - 8 3 2 + ∫ 0 2 π 3 1 + cos ⁡ u d u =

= 4 π 3 - 8 3 2 + u + sin ⁡ u 2 π 3 0 = 4 π 3 - 8 3 2 + 2 π 3 + 3 2 = 4 π + 2 π 3 - 8 3 + 3   2 =

= 2 π - 7 3   2

Á r e a   2 = 1 2 ∫ π 3 5 π 3 ( 1 ) 2 d θ = 1 2 × 1 × 5 π 3 - π 3 = 1 2 × 4 π 3 = 2 π 3

Passo 3

Agora somamos:

2 π - 7 3   2 + 2 π 3 = 6 π + 2 π 3 - 7 3 2 = 8 π 6 - 7 3 2

Resposta

Á r e a = 1 2 ∫ - π 3 π 3 4 1 - cos ⁡ θ 2 d θ + 1 2 ∫ π 2 5 π 3 3 2 d θ = 8 π 6 - 7 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da
Dois carros de corrida, lado a lado em uma pista reta, movem-se com funções velocidade v 1 t m / s e v 2 m / s , respectivamente. Suponha que ambos estejam alinhados no instante t = 60s . Interprete o
Encontre a região englobada pela curva y = s e nx e a reta que passa pelos pontos ( 0,0 ) e 5 π 6 , 1 2 na curva.
Encontre uma reta vertical x = k que divida a área englobada pelas curvas x = y , x = 2 e y = 0 em duas partes iguais.
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da