Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 51
Encontre as assindotas horizontal e vertical de cada curva. Se você tiver um dispositivo gráfico, confira pela curva gráfica as assindotas estimadas:
Passo 1
Opa, vamos fazer essa questão! Temos a seguinte curva:
E o enunciado pede pra a gente encontrar as suas as assíntotas horizontais e verticais e depois confirmar que o cálculo está certo esboçando o gráfico da função!
Para acharmos as assíntotas horizontais, vamos analisar os limites para tendendo a e . Se esses limites forem finitos, temos assíntotas horizontais.
Já as assíntotas verticais geralmente estão relacionados a pontos onde a nossa função não esta definida. Nesses pontos, se a função for pro infinito, temos assíntotas verticais.
Bora colocar a mão na massa então!
Passo 2
Começando pelas assíntotas horizontais, vamos analisar os limites para e .
Concorda comigo que quando temos:
Então vamos reescrever o nosso limite assim:
Ou seja, não temos assíntota horizontal!
Passo 3
Para calcular a assíntota vertical a gente vai atrás de pontos onde a função não pode ser calculada:
Nesse caso não podemos ter o denominador igual a zero, então:
Esses são nossos pontos candidatos pra assíntotas verticais. Vamos calcular pra conferir:
Não temos assíntota em
Opa! Aqui vai pra infinito!
Portanto apenas é uma assíntota vertical!
Passo 4
Agora vamos ver o gráfico pra conferir!
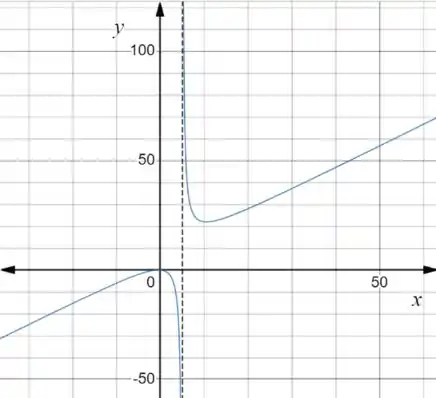
Certinho!!