Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.3 - Ex. 46
- Encontre as assíntotas vertical e horizontal.
- Encontre os intervalos nos quais a função é crescente ou decrescente.
- Encontre os valores de máximo e mínimo locais
- Encontre os intervalos de concavidade e os pontos de inflexão.
- Use as informações das partes (a)-(d) para esboçar o gráfico de
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”
Bora atacar esse problemaaaaaaa junto comigoo.
Vamos resolver a questão pedida, que envolve a análise da função
A questão pede para analisar a função em vários aspectos:
Assíntotas verticais: Elas acontecem quando tende a infinito, pra isso a gente tem que pensar em valores de que são problemáticos na função. Nessa daqui a gente vai Iidentificar os valores de onde o denominador da função é igual a zero. se anula.
Assíntotas horizontais: Analisar o comportamento da função quando tende a .
Intervalos de crescimento e decrescimento: Encontrar os pontos críticos através da derivada primeira e analisar o sinal da derivada para determinar os intervalos.
Máximos e mínimos locais: Usar os pontos críticos e a derivada segunda ou o teste da primeira derivada para determinar a natureza dos pontos críticos.
Concavidade e pontos de inflexão: Calcular a derivada segunda e analisar seu sinal para identificar intervalos de concavidade e pontos de inflexão.
Passo 2
Agora iremos relacionar o que foi dado com o que está pedindo, it’s okay?
- A função dada é
Vamos procurar as Aassíntotas verticais e horizontais!
Assíntota vertical:
A assíntota vertical ocorre onde o denominador é zero, ou seja, quando:
Então temos que:
Portanto, há uma assíntota vertical em
Assíntota horizontal:
Para encontrar a assíntota horizontal, analisamos o limite da função quando tende a
Isolando o :
Portanto, a assíntota horizontal é
Passo 3
Agora vamos verificar os Iintervalos de crescimento e decrescimento da função.
Calculamos a Pprimeira derivada:
Usando a regra do quociente:
Derivando:
Podemos rearranjar:
Ficamos então com:
Para determinar os intervalos de crescimento e decrescimento, analisamos o sinal de
- quando:
- quando:
Essas desigualdades devem ser analisadas considerando o comportamento dos sinais de
Passo 4
Valores de máximo e mínimo locais
Para encontrar os pontos críticos, igualamos a primeira derivada a zero:
Precisamos analisar o comportamento de ao redor de
Passo 5
Intervalos de concavidade e pontos de inflexão
Segunda derivada:
Usamos
e aplicamos a regra do quociente novamente:
Para determinar os intervalos de concavidade, analisamos o sinal de
- (concavidade para cima)
- (concavidade para baixo)
Passo 6
Esboço do gráfico da função
Usamos todas as informações obtidas para esboçar o gráfico:
1. A assíntota vertical está em
2. A assíntota horizontal está em
3. A função tem um ponto crítico em e precisa ser analisado para determinar se é um máximo ou mínimo.
4. Analisamos os sinais das derivadas primeira e segunda para determinar os intervalos de crescimento, decrescimento, concavidade e pontos de inflexão.
Combinar essas informações nos permitirá esboçar o gráfico final de
Podemos agora esboçar o gráfico com base nas informações obtidas.
Passo 7
Aqui está o gráfico
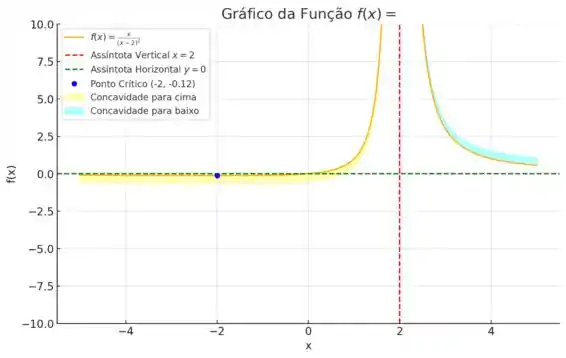
Assíntota Vertical: Existe uma assíntota vertical em indicada pela linha tracejada vermelha.
Assíntota Horizontal: Existe uma assíntota horizontal em indicada pela linha tracejada verde.
Ponto Crítico: O ponto crítico foi identificado em .
Concavidade:
- Concavidade para cima (amarela): Nas regiões onde a segunda derivada é positiva.
- Concavidade para baixo (azul): Nas regiões onde a segunda derivada é negativa.
“Às vezes é preciso aprender a correr antes de começar a andar”
Resposta
Vide o passo a passo.