Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.6 - Ex. 34
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e de mínimo e os pontos de inflexão movem-se quando varia. Você também deve identificar o valor intermediário de no qual o aspecto básico da curva mude.
Passo 1
Vamos analisar os gráficos de
Quando é negativo,
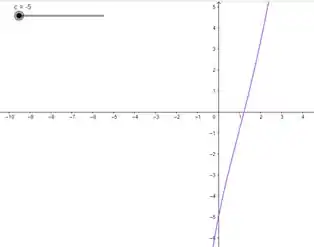
Quando
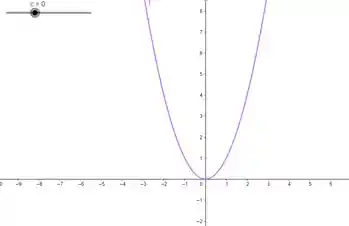
Quando
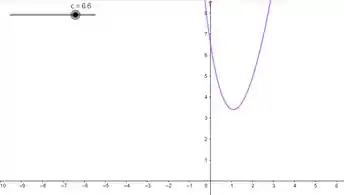
Passo 2
Agora vamos fazer nossa analise...
Quando ,a função não apresenta máximos e nem mínimo, mas a medida que se torna positivo, a função começa a apresentar mínimo cada vez mais distante do eixo . Quando , há um ponto de inflexão, porém a medida que se torna positivo, o ponto de inflexão desparece . O aspecto da curva muda quando , a partir daí ela se torna uma pabola.
Resposta
Quando ,a função não apresenta máximos e nem mínimo, mas a medida que se torna positivo, a função começa a apresentar mínimo cada vez mais distante do eixo . Quando , há um ponto de inflexão, porém a medida que se torna positivo, o ponto de inflexão desparece . O aspecto da curva muda quando , a partir daí ela se torna uma pabola.