Faça gráficos de que revelem todos os aspectos importantes a curva encontrar e . Utilize os gráficos destas derivadas para estimar os intervalos de crescimento, valores extremos e intervalos de concavidade e pontos de inflexão de
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão dá pra gente a curva
E pede pra gente fazer seu gráfico de que revele todos os seus aspectos importantes.
Para isso devemos usar os gráficos de e para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão da função .
Então a ideia aqui é a gente relembrar o que cada uma dessas derivadas pode nos trazer de informações, assim poderemos traçar o gráfico de com todas as características necessárias.
Então vamos lembrar o que cada derivada conta pra gente.
A derivada de uma função é entendida como a inclinação da reta tangente a curva do gráfico da função.
Sabendo disso, podemos pensar que quanto mais positiva a derivada estiver, mais rapidamente a função original estará crescendo.
Assim:

Já a derivada de segunda ordem é a inclinação da reta tangente ao gráfico da primeira derivada e ela nos trará informações sobre o sentido da concavidade.
Assim:
![]()
O ponto de inflexão acontece onde a derivada de segunda ordem for igual a zero. Assim:
Agora que já sabemos de tudo isso, bora resolver essa questão.
Para resolvermos este problema, é ideal que façamos primeiramente as derivações necessárias e encontremos os pontos de interseção com o eixo para em seguida, esboçarmos os gráficos, okay?
Passo 2
Vamos usar o software geogebra. Na janela de álgebra vamos usar a função
e plotar o gráfico de
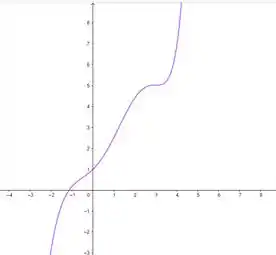
Calculando sua derivada, teremos:
Assim,
E vamos plotar o gráfico de
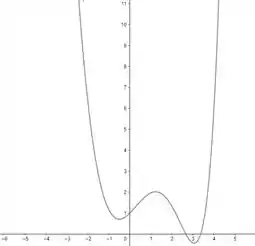
Perceba que é crescente em e e decrescente em
O que nos diz que atinge um máximo em e mínimo em
Passo 3
Agora derivando a novamente a função, teremos:
Plotando o gráfico de
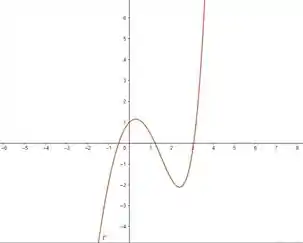
Temos que é côncava para baixo em e côncava para cima em
Pelo gráfico, temos dois pontos de inflexão em .
Existem um ponto de inflexão .
Resposta
é crescente em e e decrescente em
atinge um máximo em e mínimo em
é côncava para baixo em e côncava para cima em
Existem um ponto de inflexão .