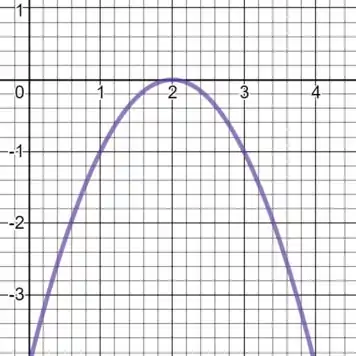
Esboce o gráfico:

Nesse caso, dentro da potência temos uma diferença, e não um termo único, então para que tivéssemos uma parábola “tradicional” () deveríamos somar a cada ponto do eixo e trocar o sinal do quadrado.

Como nesse caso o termo está sendo multiplicado por então temos uma concavidade voltada para baixo e que para cada valor de temos um valor de que é o quadrado de seu valor multiplicado por menos um. Em outras palavra, o sinal negativo inverte o gráfico do em relação ao eixo .

Para traçarmos a curva, devemos então pegar a parábola e somar uma unidade em cada ponto do eixo , ou seja, deslocar a parábola para a direira em uma unidade de é virar a parábola de cabeça ora baixo.