Esboce o gráfico:
Passo 1
Para esboçarmos o gráfico de devemos lembrar que o grafico de qualquer função do segundo grau é sembre uma parábola, e o coeficiente que muitiplica o quadrado é respesável por definir se a concavidade é pra baixo ( se for negativo) ou para cima (se for positivo).
Como nesse caso esse coeficiente é (que é negativo) então temos uma concavidade voltada para baixo e que para cada valor de temos um valor de que é o seu quadrado multiplicado por menos um. Em outras palavras, o sinal negativo inverte o gráfico do em relação ao eixo .
Passo 2
Assim, temos os gráfico:
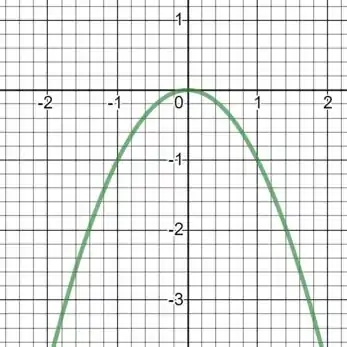
Resposta
Ei, a resposta está no passo a passo :)