Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 39
Encontre o domínio e o intervalo e esboce o gráfico da função.
Passo 1
Fala galera, tudo bem? O problema nos dá essa função
E pede para encontrarmos o domínio dela e ainda esboçar o gráfico da função!
Bom pessoal, para encontrar o domínio desta função, temos que ver para quais valores de x a função está definida.
De forma mais simples, podemos ver se existe algum valor de x para qual a função dá problema. Mas o que é dar problema?
Dar problema pode ser por exemplo um denominador ser zero, uma raiz quadrada ser negativa, etc.
Então a ideia é olhar com carinho pra função e ver se ela apresenta alguma indeterminação. Caso ela não apresentar, então todos os que estão no conjunto dos reais funcionam!
E o esboço? Aí é papo para mais tarde, já já chegamos lá!
Bora começar?
Passo 2
Nossa função
Chamamos função do tipo de linear: polinômio de grau um.
No caso da função mostrada, não há nenhum impedimento para qualquer valor de x. Então seu domínio será todos os reais.
Podemos escrever assim também
Pois pertence ao conjunto dos reais! Sem nenhuma restrição!
Beleza?
Passo 3
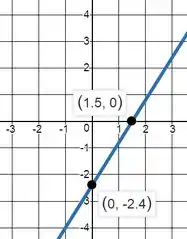
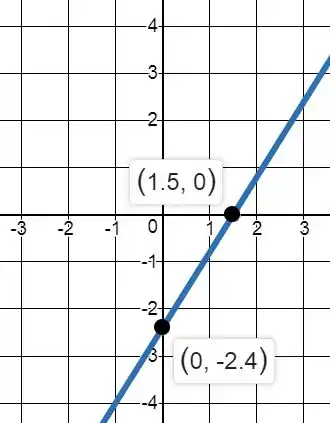
Para esboçar o gráfico da função, podemos encontrar alguns pontos e depois traçar a curva que passa por eles. Por ser uma equação do primeiro grau, é uma reta.
Então bastam 2 pontos para definir como será o gráfico. Vamos então aos pontos quando x = 0, e quando y = 0:
Plotando esses dois pontos e traçando uma reta entre eles temos essa reta em azul:
Beleza? Espero ter ajudado!
Resposta
