Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 45
Encontre a equação para a cônica que satisfaz as condições dadas.
45. Hipérbole, vértices , , focos
Passo 1
Eaee!! Tudo certinho?? Bom... o enunciado quer que encontremos a equação para uma cônica.
Para isso, ele nos dá três condições:
- Trata-se de uma hipérbole;
- Possui focos em e ;
- Tem vértices em e .
Para resolvermos isso, temos que saber do que trata-se uma hipérbole.
Bom... para respondermos isso temos que analisar a figura da hipérbole abaixo:
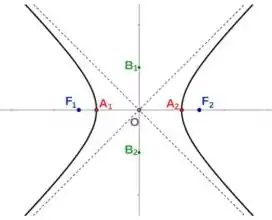
Nessa figura temos que:
- e são os focos;
- e são os vértices;
- As retas pontilhadas são as assíntotas;
- A distância do centro a um dos focos é dada por ;
- A distância do centro a um dos vértices é dada por ;
- A distância do centro a um dos conjugados é dada por .
Temos também que:
Também sabemos que a equação geral que descreve uma hipérbole centrada na origem é dada por:
Agora vamos aplicar esses conceitos!! 😉
Passo 2
Tanto os vértices quanto os focos possuem coordenada , o que significa que a equação da hipérbole será do tipo:
Como podemos perceber também, os focos não estão em posições simétricas.
Assim, precisamos então encontrar a posição do centro em relação ao eixo também.
Para isso, vamos fazer a diferença entre as coordenadas dos vértices (poderia ser dos focos):
E então dividimos por :
Ao somarmos ao vértice , ficamos com , que será a posição do centro, então:
Agora sabemos o quanto o centro foi transladado para cima, e a equação se torna:
Passo 3
Como os focos distam unidades do centro, então:
Pela equação de , basta substituir os valores que encontramos para calcular :
Assim, a equação da hipérbole então será: