Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.1 - Ex. 54
Determine se a sequência converge ou diverge. Se convergir, encontre o limite.
Passo 1
Galerinha, uma sequência tem limite e escrevemos
se conseguirmos fazer os termos de chegarem mais próximos de usando um valor para suficientemente grande. Se esse limite existe, podemos dizer que a sequência converge. Caso contrário, a sequência diverge. Que tal, então, aplicarmos isso a nossa questão? Vamos ver se existe o limite da sequência que nos foi dada!
E para isso podemos usar o teorema do confronto! Esse teorema nos diz que se nossa sequência estiver entre duas outras funções, e essas funções denderem a zero, quer dizer que nossa sequência também tende a zero
E assim nossa sequência seria convergente! Então a ideia é ver se encontramos duas funções para ajudar a gente!
Bora começar?
Passo 2
Vamos pegar essa sequência e jogar num plano cartesiano, beleza?
Será que temos uma função que estaria por cima e outra por baixo? Vamos olhar com carinho nossa sequência
Podemos cercar esses pontos por duas funções: em cima e . A figura abaixo mostra essa situação.
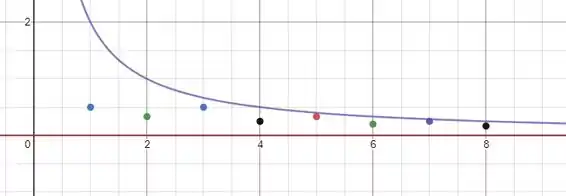
Uma sequência que está entre outras duas pode ter seu limite calculado através do teorema do Confronto! Assim, vamos calcular primeiro o limite da função de cima:
Agora, para a função de baixo:
Assim, pelo teorema do Confronto, o valor do limite também é igual a zero, mostrando assim que a sequência converge!
Resposta
A série converge para zero!