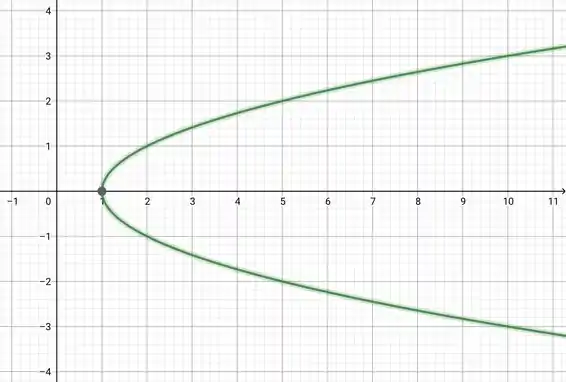
Desenhe um esboço do gráfico da equação:
Passo 1
Para esboçar o gráfico de uma equação, precisamos saber o tipo de gráfico que ela representa. Para isso, observamos as potências de x e de y na equação e comparamos com as equações básicas que nós sabemos, como , , , , entre outras que conhecemos. Depois é só deslocar o gráfico base em a unidades para a esquerda, para a direita, para baixo ou para cima, respectivamente, quando substituímos x por ou y por , e ainda alongar ou contrair o gráfico caso tenha alguma constante multiplicando as variáveis.
Passo 2
Nesse caso, analisaremos a equação base , ou seja, uma parábola “deitada”. Dessa forma, o gráfico base será:
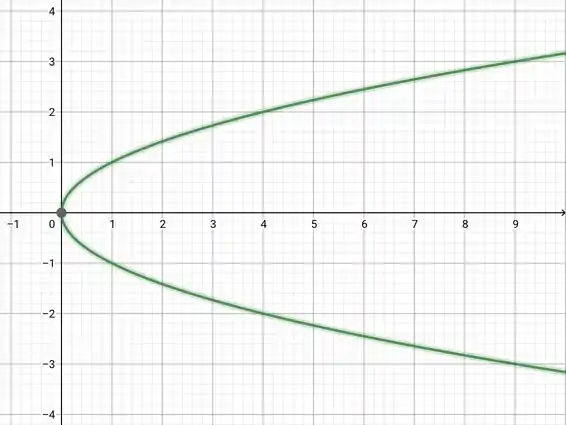
Passo 3
Substituindo x por , deslocamos o gráfico uma unidade para a direita, então,
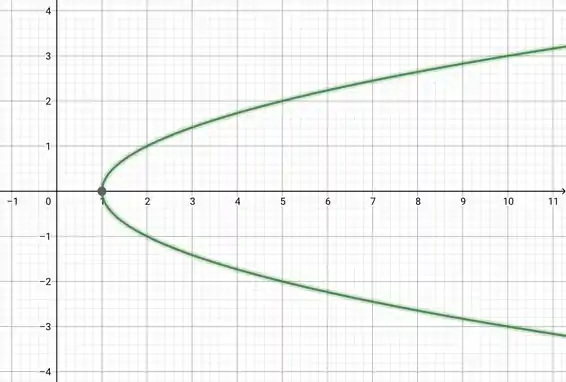
Resposta