Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 48
Encontre a equação para a cônica que satisfaz as condições dadas.
48. Hipérbole, focos , , assíntotas e
Passo 1
Eaee!! Tudo certinho?? Bom... o enunciado quer que encontremos a equação para uma cônica.
Para isso, ele nos dá três condições:
- Trata-se de uma hipérbole;
- Possui focos em e ;
- Tem assíntotas e .
Para resolvermos isso, temos que saber do que trata-se uma hipérbole.
Bom... para respondermos isso temos que analisar a figura da hipérbole abaixo:
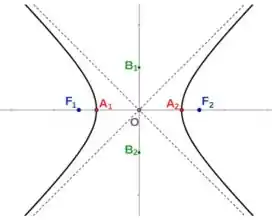
Nessa figura temos que:
- e são os focos;
- e são os vértices;
- As retas pontilhadas são as assíntotas;
- A distância do centro a um dos focos é dada por ;
- A distância do centro a um dos vértices é dada por ;
- A distância do centro a um dos conjugados é dada por .
Temos também que:
Também sabemos que a equação geral que descreve uma hipérbole centrada na origem é dada por:
Agora vamos aplicar esses conceitos!! 😉
Passo 2
Os focos estão na mesma reta com , o que significa que a equação da hipérbole começará com a seguinte cara:
Como sabemos que o centro da hipérbole foi transladado para , precisamos organizar as equações das assíntotas de maneira a ficarem com essa condição.
Primeiro vamos organizar a assíntota:
Subtraindo nos dois lados:
Tirando fator comum:
E agora a outra assíntota:
Subtraindo :
Tirando fator comum:
Concluímos então que o centro da hipérbole foi transladado para , a equação então se torna:
Passo 3
Para calcularmos e , vamos utilizar a definição das assíntotas:
E compará-la com uma das assíntotas que calculamos, para encontrar o valor de :
Como ainda não temos o que precisamos, vamos buscar outra equação pelo valor dos focos para conseguirmos e .
Com o valor dos focos podemos encontrar o valor de , basta calcularmos a distância entre eles e dividirmos por :
E pela equação de :
Como a relação anterior nos dá:
Basta substituirmos:
E elevando a relação ao quadrado:
Ao substituirmos , teremos:
Assim, substituindo na equação da hipérbole: