Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 35
Encontre a equação para a cônica que satisfaz as condições dadas.
35. Parábola, vértice , eixo horizontal passando por .
Passo 1
Oiii, tudo tranquilinho?? Bom... o enunciado quer que encontremos a equação para uma cônica.
Para isso, ele nos dá três condições:
- Trata-se de uma parábola;
- Eixo horizontal passando por ;
- Tem vértice em .
Para resolvermos isso, temos que saber do que trata-se uma parábola.
Bom... seja a seguinte parábola:
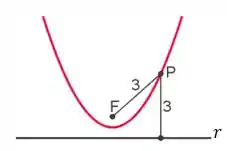
- O ponto é chamado de foco e determina essa figura;
- A reta é chamada de diretriz da parábola. A distância entre qualquer ponto da parábola e a sua diretriz é igual à distância entre esse mesmo ponto da parábola e o seu foco;
- O vértice da parábola é o ponto mais próximo de sua diretriz.
Assim, temos a equação padrão da parábola:
Esse valor determina a distância focal da parábola, bem como a direção em que a parábola se abre.
Agora que já sabemos os conceitos, vamos aplicar!! 😉
Passo 2
Considerado as translações do vértice em , podemos aplicar na nossa equação padrão:
Como o eixo passa por , podemos substituir esses valores na equação acima para encontrarmos :
Passo 3
Substituindo o valor que encontramos na equação do Passo 1:
Essa será a equação da parábola.