Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 54

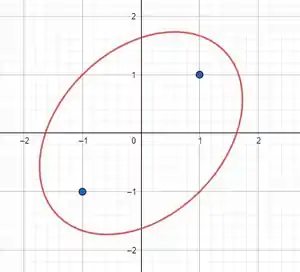
Encontre uma equação para a elipse com focos ( 1,1 ) e ( - 1 , - 1 ) e eixo maior com comprimento igual a 4 .

Passo 1

Olá, meu amigo. Vou te ajudar a resolver essa atividade.

A gente precisa encontrar aqui uma equação para elipse com as informações que nos foram dadas.

O foco fica em:

1,1

E

- 1 , - 1

O eixo maior tem o comprimento de 4 .

Passo 2

Lembrando da definição de elipse, sabemos que

P F 1 + P F 2 = a

onde P é um ponto qualquer pertencente a elipse e a é seu eixo maior.

Então basta substituirmos nossos pontos nessa equação:

x - 1 2 + y - 1 2 + x + 1 2 + y + 1 2 = 4

x - 1 2 + y - 1 2 = 4 - x + 1 2 + y + 1 2

Elevando os dois lados ao quadrado:

x - 1 2 + y - 1 2 = 16 - 8 x + 1 2 + y + 1 2 + x + 1 2 + y + 1 2

Desenvolvendo os produtos notáveis:

x 2 - 2 x + 1 + y 2 - 2 y + 1 = 16 - 8 x + 1 2 + y + 1 2 + x 2 + 2 x + 1 + y 2 + 2 y + 1

Simplificando os termos semelhantes:

- 2 x - 2 y = 16 + 2 x + 2 y - 8 x + 1 2 + y + 1 2

- 4 x + y - 16 = - 8 x + 1 2 + y + 1 2

x + y + 4 = 2 x + 1 2 + y + 1 2

Vamos elevar ao quadrado dos dois lados mais uma vez:

x + y 2 + 16 + 8 ( x + y ) = 4 [ x + 1 2 + y + 1 2 ]

x 2 + y 2 + 2 x y + 16 + 8 x + 8 y = 4 [ x 2 + 2 x + 1 + y 2 + 2 y + 1 ]

x 2 + y 2 + 2 x y + 16 + 8 x + 8 y = 4 x 2 + 8 x + 4 + 4 y 2 + 8 y + 4

2 x y + 8 = 3 x 2 + 3 y 2

Essa é a equação que estávamos procurando, ela é bem diferentona das outras equações de elipse né? É porque ela está rotacionada, e não com o eixo coincidindo com os eixos ordenados, como estamos acostumados. Dá uma olhada no seu gráfico:

Resposta

2 x y + 8 = 3 x 2 + 3 y 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a equação para a cônica que satisfaz as condições dadas.38. Elipse, focos ( 0 ,± 2 ) , vértices ( 0 ,± 2 )
Encontre a equação para a cônica que satisfaz as condições dadas.45. Hipérbole, vértices ( - 3 ,- 4 ) , ( - 3 ,6 ) , focos - 3 ,- 7 , ( - 3 , 9 )
Encontre a equação para a cônica que satisfaz as condições dadas.40. Elipse, focos 0 ,- 1 ,( 8 ,- 1 ) vértice ( 9 ,- 1 )
Escreva a equação polar da cônica com o foco na origem e com as informações dadas3. Hipérbole, excentricidade 1.5 , diretriz y = 2
Escreva a equação polar da cônica com o foco na origem e com as informações dadas1. Elipse, excentricidade 1 2 , diretriz x = 4 .