Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios adicionais e avançados - Ex. 1
Encontre uma equação para a parábola com foco e diretriz . Esboce a parábola com seu vértice, seu foco e sua diretriz.
Passo 1
Vem comigo pessoal!!
Relembrando que uma parábola é um conjunto que consiste de todos os pontos em um plano equidistantes de um ponto fixo e de uma dada reta fixa no plano. O ponto fixo é o foco da parábola. A reta fixa é a diretriz.
A equação genérica da parábola é dada por:
Primeiramente precisamos encontrar o nosso vértice. O vértice fica entre o foco e a diretriz:
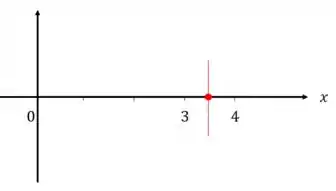
Sendo assim, nosso vértice é no ponto . E o ponto é o tamanho do foco até a diretriz, ou seja, .
Passo 2
Substituindo esses valores na equação da parábola:
Sendo assim, conseguimos construir a seguinte parábola:
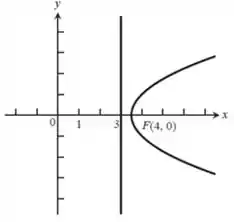
Resposta
.
Exercícios de Livros Relacionados
No exercício a seguir, o gráfico da equação é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o gráfi
No exercício a seguir, o gráfico da equação é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o gráfi
No exercício a seguir, o gráfico da equação é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o gráfi
No exercício a seguir, ache a equação da hipérbole com as propriedades dadas e faça um esboço do gráfico.Centro em (-5,2), um Vértice em (-1,2) e um foco em (0,2)
Qualquer secção de um espelho parabólico feita por um plano que passa pelo eixo do espelho é um segmento de parábola. A altura do segmento é 12 cm e o comprimento da base é 18 cm. Uma secção do espelh